题目内容
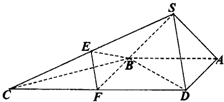 如图,等腰直角三角形SAB所在平面与直角梯形ABCD所在平面垂直,SA=SB=
如图,等腰直角三角形SAB所在平面与直角梯形ABCD所在平面垂直,SA=SB=| 2 |
(I)求证:平面BEF∥平面SAD;
(Ⅱ)求二面角S-BD-F的余弦值.
分析:(I)利用等腰直角三角形的性质、三角形的中位线定理、平行四边形的性质和面面平行的判定定理即可得出;
(II)取AB的中点H,连接SH,则SH⊥AB,利用面面垂直的性质及平面SAB⊥平面ABCD,可得SH⊥平面ABCD.
作HG⊥BD于G点,连接SG,利用三垂线定哩可得SG⊥BD.于是得到∠SGH是二面角S-BD-F的平面角.求出即可.
(II)取AB的中点H,连接SH,则SH⊥AB,利用面面垂直的性质及平面SAB⊥平面ABCD,可得SH⊥平面ABCD.
作HG⊥BD于G点,连接SG,利用三垂线定哩可得SG⊥BD.于是得到∠SGH是二面角S-BD-F的平面角.求出即可.
解答:(I)证明:∵E、F分别是线段SC、CD的中点,∴EF∥SD.
∵△SAB是等腰直角三角形,且SA=SB=
,∴AB=
SA=
×
=2.
∵DF=
CD=2,AB∥CD,
∴四边形ABFD是平行四边形,∴BF∥AD.
又∵EF∩BF=F,
∴平面BEF∥平面SAD;
(II)解:取AB的中点H,连接SH,则SH⊥AB,
∵平面SAB⊥平面ABCD,∴SH⊥平面ABCD.
作HG⊥BD于G点,连接SG,则SG⊥BD.
∴∠SGH是二面角S-BD-F的平面角.
∵AB=AD,AD⊥AB,∴∠GBH=45°,
∵SH=BH=1,∴HG=
,
∴tan∠SGH=
=
,
∴cos∠SGH=
.
∵△SAB是等腰直角三角形,且SA=SB=
| 2 |
| 2 |
| 2 |
| 2 |
∵DF=
| 1 |
| 2 |
∴四边形ABFD是平行四边形,∴BF∥AD.
又∵EF∩BF=F,
∴平面BEF∥平面SAD;
(II)解:取AB的中点H,连接SH,则SH⊥AB,
∵平面SAB⊥平面ABCD,∴SH⊥平面ABCD.
作HG⊥BD于G点,连接SG,则SG⊥BD.
∴∠SGH是二面角S-BD-F的平面角.
∵AB=AD,AD⊥AB,∴∠GBH=45°,
∵SH=BH=1,∴HG=
| ||
| 2 |
∴tan∠SGH=
| SH |
| GH |
| 2 |
∴cos∠SGH=
| ||
| 3 |
点评:熟练掌握等腰直角三角形的性质、三角形的中位线定理、平行四边形的性质和面面平行的判定定理、面面垂直的性质、三垂线定理、二面角的作法等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
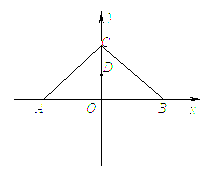
 (Ⅱ)求CN与平面ABD所成角的正弦值.
(Ⅱ)求CN与平面ABD所成角的正弦值.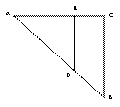
 如图,等腰直角三角形△O′A′B′是△AOB的直观图,∠B′=90°,它的斜边长为O′A′=a,求△AOB的面积.
如图,等腰直角三角形△O′A′B′是△AOB的直观图,∠B′=90°,它的斜边长为O′A′=a,求△AOB的面积. ,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为
,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为 ,
,