题目内容
17.已知函数$f(x)=\left\{\begin{array}{l}ax+2-3a\;,x<0\\{2^x}-1\;\;,\;\;\;x≥0.\end{array}\right.$若存在x1,x2∈R,x1≠x2,使f(x1)=f(x2)成立,则实数a的取值范围是(-∞,$\frac{2}{3}$).分析 当x≥0时,2x-1≥0,故若存在x1,x2∈R,x1≠x2,使f(x1)=f(x2)成立,则当x<0时,存在不小于0的函数值,进而得到答案.
解答 解:当x≥0时,2x-1≥0,
当x<0时,
若a=0,则f(x)=2恒成立,满足条件;
若a>0,则f(x)<2-3a,若存在x1,x2∈R,x1≠x2,使f(x1)=f(x2)成立,则2-3a>0,
即a∈(0,$\frac{2}{3}$);
若a>0,则f(x)<2-3a,若存在x1,x2∈R,x1≠x2,使f(x1)=f(x2)成立,则2-3a>0,
即a∈(0,$\frac{2}{3}$);
若a<0,则f(x)>2-3a,满足条件,
综上可得:a∈(-∞,$\frac{2}{3}$);
故答案为:(-∞,$\frac{2}{3}$)
点评 本题考查的知识点是分段函数的应用,函数求值,函数的图象和性质,难度中档.

练习册系列答案
相关题目
8.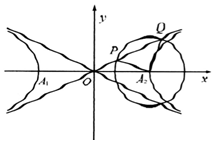 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
12.已知函数$f(x)=2-\frac{3}{x}$,若g(x)=f(x)-m为奇函数,则实数m的值为( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
9.某市家庭煤气的使用量x(m3)和煤气费f(x)(元) 满足关系f(x)=$\left\{\begin{array}{l}{C,0<x≤A}\\{C+B(x-A),x>A}\end{array}\right.$,已知某家庭今年前三个月的煤气费如表:
若四月份该家庭使用了20m3的煤气,则其煤气费为( )元.
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4 元 |
| 二月份 | 25m3 | 14 元 |
| 三月份 | 35m3 | 19 元 |
| A. | 10.5 | B. | 10 | C. | 11.5 | D. | 11 |
5.抛物线y2=8x的焦点为F,设A(x1,y1),B(x2,y2)是抛物线上的两个动点,若x1+x2+4=$\frac{{2\sqrt{3}}}{3}|{AB}$|,
则∠AFB的最大值为( )
则∠AFB的最大值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
 ,则
,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.