题目内容
12.已知$\frac{sin(2π-α)cos(π+α)}{cos(π-α)sin(3π-α)sin(-π-α)}$=3,求tan(5π-α)的值.分析 已知等式左边利用诱导公式化简,约分求出sinα的值,利用同角三角函数间的基本关系求出tanα的值,原式利用诱导公式化简,代入计算即可求出值.
解答 解:由$\frac{sin(2π-α)cos(π+α)}{cos(π-α)sin(3π-α)sin(-π-α)}$=3,化简得:$\frac{-sinα•(-cosα)}{-cosα•sinα•sinα}$=-$\frac{1}{sinα}$=3,即sinα=-$\frac{1}{3}$,
∴cos2α=1-sin2α=$\frac{8}{9}$,
∴tan2α=$\frac{1}{1+co{s}^{2}α}$=$\frac{9}{17}$,即tanα=±$\frac{3\sqrt{17}}{17}$,
则tan(5π-α)=-tanα=±$\frac{3\sqrt{17}}{17}$.
点评 此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
7.等差数列{an}的首项a1=-5,它的前11项平均值为5,若从中抽去一项,余下的平均值为4.6,则抽去的是( )
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
17.若复数z满足|z|=1,则|z-3-4i|的最小值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.已知实数x.y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x<2}\\{x+y-1≥0}\end{array}\right.$,z=|4x-4y+3|,则z的取值范围是( )
| A. | [$\frac{5}{3}$,15] | B. | [$\frac{5}{3}$,15) | C. | [$\frac{5}{3}$,5) | D. | (5,15) |
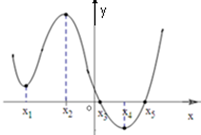 如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处
如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处