题目内容
若对任意的x>0,恒有lnx≤px-1(p>0),则p的取值范围是
- A.(0,1]
- B.(1,+∞)
- C.(0,1)
- D.[1,+∞)
D
分析:先把lnx≤px-1转化为p≥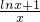 恒成立,再利用导函数求函数f(x)=
恒成立,再利用导函数求函数f(x)=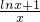 的最大值,让p与其最大值比较即可.
的最大值,让p与其最大值比较即可.
解答:因为对任意的x>0,恒有lnx≤px-1?p≥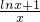 恒成立,
恒成立,
设f(x)=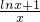 只须求其最大值,
只须求其最大值,
因为f'(x)=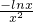 ,令f'(x)=0?x=1,
,令f'(x)=0?x=1,
当0<x<1时,f'(x)>0,
当x>1时,f'(x)<0,
故f(x)在x=1处取最大值且f(1)=1.
故p的取值范围是[1,+∞).
故选 D.
点评:在解决恒成立问题时,一般常用转化思想,比如本题就是把lnx≤px-1转化为p≥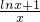 恒成立.
恒成立.
分析:先把lnx≤px-1转化为p≥
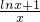 恒成立,再利用导函数求函数f(x)=
恒成立,再利用导函数求函数f(x)=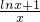 的最大值,让p与其最大值比较即可.
的最大值,让p与其最大值比较即可.解答:因为对任意的x>0,恒有lnx≤px-1?p≥
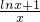 恒成立,
恒成立,设f(x)=
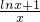 只须求其最大值,
只须求其最大值,因为f'(x)=
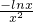 ,令f'(x)=0?x=1,
,令f'(x)=0?x=1,当0<x<1时,f'(x)>0,
当x>1时,f'(x)<0,
故f(x)在x=1处取最大值且f(1)=1.
故p的取值范围是[1,+∞).
故选 D.
点评:在解决恒成立问题时,一般常用转化思想,比如本题就是把lnx≤px-1转化为p≥
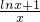 恒成立.
恒成立. 
练习册系列答案
相关题目
若对任意的x>0,恒有lnx≤px-1(p>0),则p的取值范围是( )
| A、(0,1] | B、(1,+∞) | C、(0,1) | D、[1,+∞) |