Question

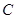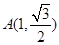已知椭圆的中心在原点，焦点在轴上．若椭圆上的点到焦点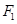、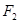的距离之和等于4．

（1）写出椭圆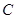的方程和焦点坐标．

（2）过点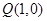的直线与椭圆交于两点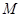、，当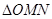的面积取得最大值时，求直线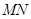的方程．

 

Answer 1

【答案】

（1），焦点坐标为，

（2）x=1

【解析】

试题分析：（1）根据椭圆的定义，由于椭圆的中心在原点，焦点在轴上．若椭圆上的点到焦点、的距离之和等于4．，则可知2a=4，a=2，同时利用定义可知，故可知椭圆的方程为椭圆C的方程为，焦点坐标为，   

（2）MN斜率不为0，设MN方程为．               

联立椭圆方程：可得

记M、N纵坐标分别为、，

则 

设

则，该式在单调递减，所以在，即时取最大值．直线方程为x=1

考点：直线与椭圆的位置关系

点评：主要是考查了直线与椭圆的位置关系的运用，属于基础题。