题目内容
圆柱轴截面的周长l为定值,那么圆柱体积的最大值是
- A.

- B.

- C.

- D.

A
分析:设出圆柱的底面半径和高,求出体积表达式,通过求导求出体积的最大值.
解答:圆柱底面半径R,高H,圆柱轴截面的周长L为定值:
4R+2H=L,
H= -2R,
-2R,
V=SH=πR2H=πR2( -2R)=πR2
-2R)=πR2 -2πR3
-2πR3
求导:
V'=πRL-6πR2令V'=0,
πRL-6πR2=0,
πR(L-6R)=0,
L-6R=0,
R=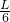 ,
,
当R=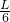 ,
,
圆柱体积的有最大值,圆柱体积的最大值是:
V=πR2 -2πR3=
-2πR3=
故选A.
点评:本题考查旋转体的体积,导数的应用,是中档题.
分析:设出圆柱的底面半径和高,求出体积表达式,通过求导求出体积的最大值.
解答:圆柱底面半径R,高H,圆柱轴截面的周长L为定值:
4R+2H=L,
H=
 -2R,
-2R,V=SH=πR2H=πR2(
 -2R)=πR2
-2R)=πR2 -2πR3
-2πR3求导:
V'=πRL-6πR2令V'=0,
πRL-6πR2=0,
πR(L-6R)=0,
L-6R=0,
R=
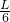 ,
,当R=
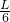 ,
,圆柱体积的有最大值,圆柱体积的最大值是:
V=πR2
 -2πR3=
-2πR3=
故选A.
点评:本题考查旋转体的体积,导数的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆柱轴截面的周长l为定值,那么圆柱体积的最大值是( )
A、(
| ||||
B、
| ||||
C、(
| ||||
D、2(
|