题目内容
(13分) 已知圆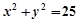 ,
,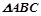 内接于此圆,
内接于此圆,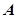 点的坐标
点的坐标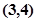 ,
,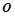 为坐标原点.
为坐标原点.
(Ⅰ)若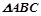 的重心是
的重心是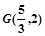 ,求直线
,求直线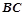 的方程;
的方程;
(Ⅱ)若直线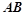 与直线
与直线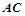 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线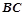 的斜率为定值.
的斜率为定值.
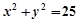 ,
,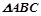 内接于此圆,
内接于此圆,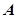 点的坐标
点的坐标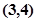 ,
,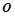 为坐标原点.
为坐标原点.(Ⅰ)若
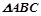 的重心是
的重心是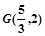 ,求直线
,求直线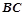 的方程;
的方程;(Ⅱ)若直线
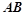 与直线
与直线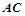 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线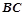 的斜率为定值.
的斜率为定值. (1)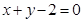 .(2)
.(2)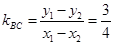 .
.
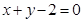 .(2)
.(2)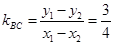 .
.(I)设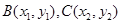 ,再由重心坐标公式可知
,再由重心坐标公式可知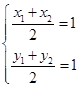 ,可得BC的中点坐标,再由
,可得BC的中点坐标,再由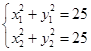 ,作差可得
,作差可得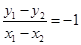 ,可得BC的斜率,进而得到BC的方程.
,可得BC的斜率,进而得到BC的方程.
(2)设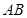 :
: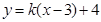 ,代入圆的方程整理得:
,代入圆的方程整理得:

由于3是上述方程的一个根,再根据韦达定理可得另一个根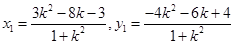 ,同理可得:
,同理可得: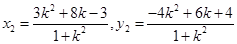 从而可求出
从而可求出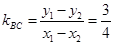
解:设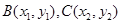
由题意可得: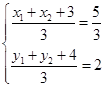 即
即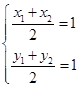 ……2分 又
……2分 又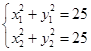
相减得: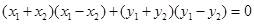
∴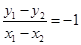 …………………4分
…………………4分
∴直线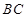 的方程为
的方程为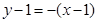 ,即
,即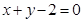 .………………6分
.………………6分
(2)设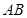 :
: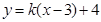 ,代入圆的方程整理得:
,代入圆的方程整理得:
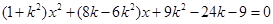
∵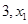 是上述方程的两根
是上述方程的两根
∴ ……………9分
……………9分
同理可得: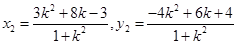 ……………11分
……………11分
∴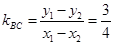 . ……………………13
. ……………………13
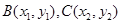 ,再由重心坐标公式可知
,再由重心坐标公式可知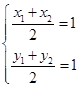 ,可得BC的中点坐标,再由
,可得BC的中点坐标,再由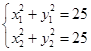 ,作差可得
,作差可得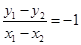 ,可得BC的斜率,进而得到BC的方程.
,可得BC的斜率,进而得到BC的方程.(2)设
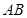 :
: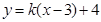 ,代入圆的方程整理得:
,代入圆的方程整理得:
由于3是上述方程的一个根,再根据韦达定理可得另一个根
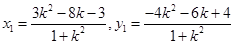 ,同理可得:
,同理可得: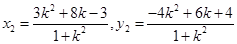 从而可求出
从而可求出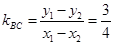
解:设
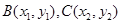
由题意可得:
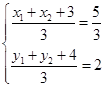 即
即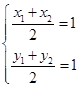 ……2分 又
……2分 又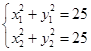
相减得:
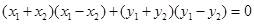
∴
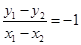 …………………4分
…………………4分∴直线
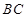 的方程为
的方程为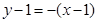 ,即
,即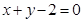 .………………6分
.………………6分(2)设
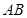 :
: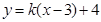 ,代入圆的方程整理得:
,代入圆的方程整理得: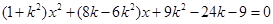
∵
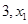 是上述方程的两根
是上述方程的两根∴
 ……………9分
……………9分同理可得:
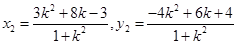 ……………11分
……………11分∴
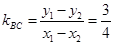 . ……………………13
. ……………………13
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
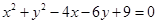 及直
及直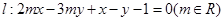
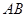 的端点
的端点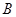 的坐标为
的坐标为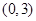 ,端点
,端点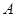 在
在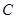 :
: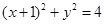 上运动。
上运动。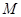 的轨迹方程;
的轨迹方程;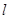 与圆
与圆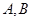 ,弦
,弦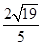 ,求直线
,求直线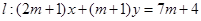 ,圆
,圆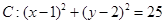
 和圆
和圆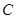 的位置关系;
的位置关系;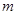 的值.
的值.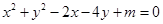 .
.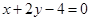 相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
相交于M、N两点,且OM⊥ON(O为坐标原点),求m;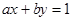 与圆
与圆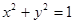 相交,则点P
相交,则点P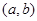 的位置是( )
的位置是( )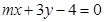 与圆
与圆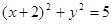 相交于
相交于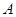 、
、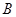 两点,若
两点,若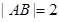 ,则实数
,则实数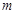 的值为( )
的值为( )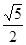
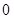 或
或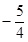

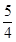
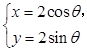 (
(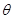 为参数),曲线C2:
为参数),曲线C2: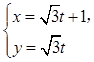 (t为参数).
(t为参数).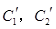 .写出
.写出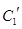 与
与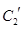 公共点的个数和C
公共点的个数和C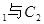 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.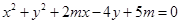 表示一个圆,
表示一个圆,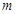 的取值范围;
的取值范围;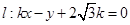 相交,求直线
相交,求直线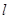 的倾斜角的取值范围.
的倾斜角的取值范围.