题目内容
已知曲线C1: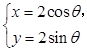 (
(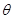 为参数),曲线C2:
为参数),曲线C2: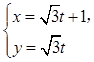 (t为参数).
(t为参数).
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都拉伸为原来的两倍,分别得到曲线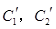 .写出
.写出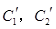 的参数方程.
的参数方程.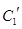 与
与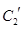 公共点的个数和C
公共点的个数和C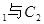 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
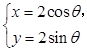 (
(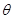 为参数),曲线C2:
为参数),曲线C2: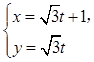 (t为参数).
(t为参数).(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都拉伸为原来的两倍,分别得到曲线
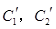 .写出
.写出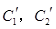 的参数方程.
的参数方程.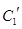 与
与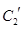 公共点的个数和C
公共点的个数和C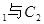 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.(1)C1是圆,C2是直线。C2与C1有两个公共点(2)C1′: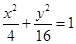 ,C2′:
,C2′: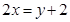 。有两个公共点,C1与C2公共点个数相同
。有两个公共点,C1与C2公共点个数相同
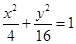 ,C2′:
,C2′: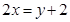 。有两个公共点,C1与C2公共点个数相同
。有两个公共点,C1与C2公共点个数相同本试题主要是考查了参数方程与极坐标方程与普通方程的转化,以及直线与椭圆的 位置关系的运用。
(1)结合已知的极坐标方程和参数方程,消去参数后得到普通方程,然后利用直线与圆的位置关系判定。
(2)拉伸后的参数方程分别为C1′: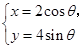 θ为参数);
θ为参数);
C2′: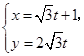 (t为参数)联立消元得
(t为参数)联立消元得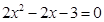 其判别式
其判别式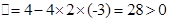 ,
,
可知有公共点。
解:(1)C1是圆,C2是直线.C1的普通方程为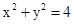 ,
,
圆心C1(0,0),半径r=2.C2的普通方程为x-y-1=0.
因为圆心C1到直线x-y+ 1=0的距离为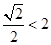 ,
,
所以C2与C1有两个公共点.
(2)拉伸后的参数方程分别为C1′: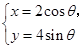 θ为参数);C2′:
θ为参数);C2′: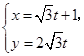 (t为参数)
(t为参数)
化为普通方程为:C1′: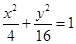 ,C2′:
,C2′: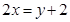
联立消元得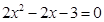 其判别式
其判别式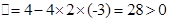 ,
,
所以压缩后的直线C2′与椭圆C1′仍然有两个公共点,和C1与C2公共点个数相同
(1)结合已知的极坐标方程和参数方程,消去参数后得到普通方程,然后利用直线与圆的位置关系判定。
(2)拉伸后的参数方程分别为C1′:
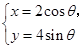 θ为参数);
θ为参数);C2′:
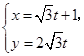 (t为参数)联立消元得
(t为参数)联立消元得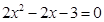 其判别式
其判别式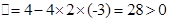 ,
,可知有公共点。
解:(1)C1是圆,C2是直线.C1的普通方程为
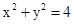 ,
,圆心C1(0,0),半径r=2.C2的普通方程为x-y-1=0.
因为圆心C1到直线x-y+ 1=0的距离为
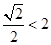 ,
,所以C2与C1有两个公共点.
(2)拉伸后的参数方程分别为C1′:
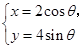 θ为参数);C2′:
θ为参数);C2′: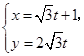 (t为参数)
(t为参数)化为普通方程为:C1′:
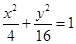 ,C2′:
,C2′: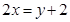
联立消元得
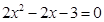 其判别式
其判别式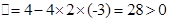 ,
,所以压缩后的直线C2′与椭圆C1′仍然有两个公共点,和C1与C2公共点个数相同

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
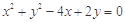 关于直线
关于直线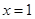 对称的圆的标准方程是____________.
对称的圆的标准方程是____________.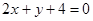 和圆
和圆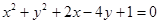 的交点,且满足下列条件之一的圆的方程. (1)过原点; (2)有最小面积.
的交点,且满足下列条件之一的圆的方程. (1)过原点; (2)有最小面积.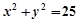 ,
,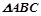 内接于此圆,
内接于此圆,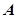 点的坐标
点的坐标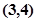 ,
,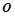 为坐标原点.
为坐标原点.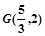 ,求直线
,求直线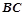 的方程;
的方程;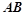 与直线
与直线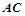 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线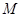 与y轴相切且与圆
与y轴相切且与圆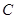 :
: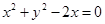 相外切, 则动圆圆心
相外切, 则动圆圆心



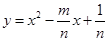 的图象在点
的图象在点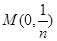 处的切线
处的切线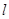 与圆
与圆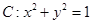 相交,则点
相交,则点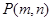 与圆
与圆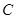 的位置关系是( )
的位置关系是( )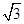 ),且斜率为1,求l与C相交所得的弦长.
),且斜率为1,求l与C相交所得的弦长.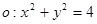 和点
和点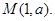
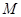 有且只有一条直线与圆
有且只有一条直线与圆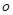 相切,求实数
相切,求实数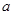 的值,并求出切线方程;
的值,并求出切线方程;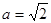 ,过点
,过点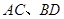 ,且
,且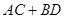 的最大值。
的最大值。 和直线
和直线 的交点在圆(x-1)2+y2=1的内部,则
的交点在圆(x-1)2+y2=1的内部,则 的取值范围是( )
的取值范围是( )
 ,0]
,0]