题目内容
设等比数列{
}的前
项和为
若
，则
＝ ( )
| A．3:4 | B．2:3 | C．1:2 | D．1:3 |
A
解析试题分析：等比数列{}中，
成等比数列，因为，所以
,可以求得
，所以=3：4.
考点：本小题主要考查等比数列的性质.
点评：等比数列中，
成等比数列这条性质经常用到，要灵活应用.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知等比数列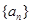
中有
，数列
是等差数列，且
，则
| A．2 | B．4 | C．8 | D．16 |
已知等比数列
满足
，则
（ ）
| A．64 | B．81 | C．128 | D．243． |
已知等比数列
的公比为正数，且
，
，则
（ ）
A． | B． | C． | D．2 |
的内角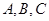
的对边分别为
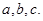若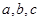
成等比数列，且
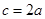，则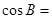
（ ）
A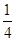． | B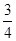． | C． | D． |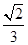
已知
是等比数列，
，且
，则
等于( )
| A．6 | B．12 | C．18 | D．24 |
设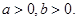
若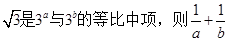
的最小值（ ）
A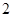． | B． | C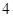． | D．8 |
等比数列｛
｝中，
，前3项之和
，则数列｛｝的公比为（ ）
| A．1 | B．1或 | C． | D．-1或 |
已知等比数列
的前n项和为
，且
，那么
的值为
A． | B． | C． | D． |