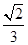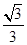题目内容
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′ 平面ABC),则下列叙述错误的是( )
平面ABC),则下列叙述错误的是( )
A. 平面A′FG⊥平面ABC
B. BC∥平面A′DE
C. 三棱锥A′-DEF的体积最大值为
D. 直线DF与直线A′E不可能共面
C
解析试题分析:对于A,由已知可得FG⊥DE, A′D⊥DE,所以DE⊥平面A′FG,又因为DE 平面ABC,所以平面A′FG⊥平面ABC ,故A正确;对于B,由BC∥DE,DE
平面ABC,所以平面A′FG⊥平面ABC ,故A正确;对于B,由BC∥DE,DE 平面A′DE, BC
平面A′DE, BC 平面A′DE,所以BC∥平面A′DE,故B正确;对于C,S
平面A′DE,所以BC∥平面A′DE,故B正确;对于C,S =
= ,当A′D⊥平面DEF时,三棱锥A′-DEF的体积取最大值,即最大值为
,当A′D⊥平面DEF时,三棱锥A′-DEF的体积取最大值,即最大值为 =
= ×
× ×
×
 ,所以C错误,故选C.
,所以C错误,故选C.
考点:1.平面与平面垂直,直线与平面平行;2.棱锥的体积.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
设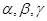 是三个互不重合的平面,
是三个互不重合的平面,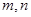 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A.若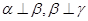 ,则 ,则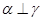 |
B.若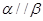 , ,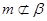 , ,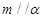 ,则 ,则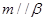 |
C.若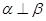 , ,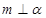 ,则 ,则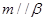 |
D.若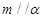 , ,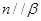 , ,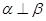 ,则 ,则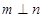 |
如图,在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中必有( )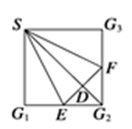
A.SG⊥△EF G所在平面 G所在平面 | B.SD⊥△EFG所在平面 |
C.GF ⊥△SEF所在平面 ⊥△SEF所在平面 | D.GD⊥△SEF所在平面 |
设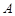 在
在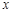 轴上,它到点
轴上,它到点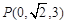 的距离等于到点
的距离等于到点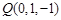 的距离的两倍,那么
的距离的两倍,那么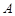 点的坐标是( )
点的坐标是( )
| A.(1,0,0)和( -1,0,0) | B.(2,0,0)和(-2,0,0) |
C.(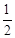 ,0,0)和( ,0,0)和(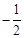 ,0,0) ,0,0) | D.(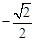 ,0,0)和( ,0,0)和( ,0,0) ,0,0) |
设 是两条直线,
是两条直线, 是两个平面,下列能推出
是两个平面,下列能推出 的是( )
的是( )
A. | B. |
C. | D. |
设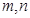 是两条不同的直线,
是两条不同的直线,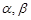 是两个不同的平面,有下列四个命题:
是两个不同的平面,有下列四个命题:
① 若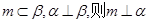 ; ② 若
; ② 若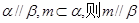 ;
;
③ 若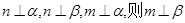 ; ④ 若
; ④ 若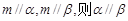
其中正确命题的序号是( )
| A.①③ | B.①② | C.③④ | D.②③ |
对于空间中的三条不同的直线,有下列三个条件:①三条直线两两平行;②三条直线共点;③有两条直线平行,第三条直线和这两条直线都相交.其中,能作为这三条直线共面的充分条件的有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
在空间中,下列命题正确的是
| A.平行于同一平面的两条直线平行 | B.垂直于同一平面的两条直线平行 |
| C.平行于同一直线的两个平面平行 | D.垂直于同一平面的两个平面平行 |