题目内容
已知函数f(x)满足f( )=log2
)=log2 ,则f(x)的解析式是________.
,则f(x)的解析式是________.
f(x)=-log2x,x∈(0,+∞)
分析:先根据对数形式将已知条件化简,再利用换元法求函数的解析式.
解答:由 可知x•|x|>0,所以x>0,
可知x•|x|>0,所以x>0,
所以 可以化简为
可以化简为 ,
,
令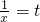 ,则t∈(0,+∞),所以有
,则t∈(0,+∞),所以有 ,
,
所以f(x)的解析式是f(x)=-log2x,x∈(0,+∞),
故答案为f(x)=-log2x,x∈(0,+∞).
点评:不要被题目的表面给迷惑,揭开外面的“面纱”后你会发现这个问题没有别出心裁之处.
分析:先根据对数形式将已知条件化简,再利用换元法求函数的解析式.
解答:由
 可知x•|x|>0,所以x>0,
可知x•|x|>0,所以x>0,所以
 可以化简为
可以化简为 ,
,令
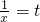 ,则t∈(0,+∞),所以有
,则t∈(0,+∞),所以有 ,
,所以f(x)的解析式是f(x)=-log2x,x∈(0,+∞),
故答案为f(x)=-log2x,x∈(0,+∞).
点评:不要被题目的表面给迷惑,揭开外面的“面纱”后你会发现这个问题没有别出心裁之处.

练习册系列答案
相关题目