题目内容
如图,三棱柱ABC-A B
B C
C 的侧面A
的侧面A ACC
ACC 与底面ABC垂直,AB=BC=CA=4,且AA
与底面ABC垂直,AB=BC=CA=4,且AA ⊥A
⊥A C,AA
C,AA =A
=A C.
C.

(Ⅰ)证明:AC⊥BA ;
;
(Ⅱ)求侧面A ABB
ABB 与底面ABC所成二面角的余弦值.
与底面ABC所成二面角的余弦值.
 B
B C
C 的侧面A
的侧面A ACC
ACC 与底面ABC垂直,AB=BC=CA=4,且AA
与底面ABC垂直,AB=BC=CA=4,且AA ⊥A
⊥A C,AA
C,AA =A
=A C.
C.
(Ⅰ)证明:AC⊥BA
 ;
;(Ⅱ)求侧面A
 ABB
ABB 与底面ABC所成二面角的余弦值.
与底面ABC所成二面角的余弦值. (1)要证明线线垂直,通过线面垂直的性质定理来证明。
(2) 侧面A ABB
ABB 与底面ABC所成的二面角为arccos
与底面ABC所成的二面角为arccos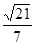
(2) 侧面A
 ABB
ABB 与底面ABC所成的二面角为arccos
与底面ABC所成的二面角为arccos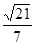
试题分析:(Ⅰ)证明:取AC的中点O,连结OA
 ,OB,BA
,OB,BA ,则
,则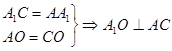 , 2分
, 2分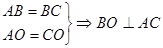 . 4分
. 4分∴AC⊥面BOA
 . 5分
. 5分∵BA

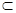 面BOA
面BOA ,∴AC⊥BA
,∴AC⊥BA . 6分
. 6分(Ⅱ)解法一:∵面A
 ACC
ACC ⊥面ABC,A
⊥面ABC,A O⊥AC,
O⊥AC,∴A
 O⊥面ABC. 7分
O⊥面ABC. 7分过点O作OH⊥AB于H,连结A
 H,则A
H,则A H⊥AB,
H⊥AB,∴∠A
 HO为所求二面角的平面角. 9分
HO为所求二面角的平面角. 9分在等边△ABC中,OH=
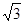 ,A
,A H=
H=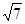 . ∴cos∠A
. ∴cos∠A HO=
HO=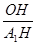 =
=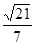 . 11分
. 11分∴侧面A
 ABB
ABB 与底面ABC所成的二面角为arccos
与底面ABC所成的二面角为arccos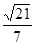 . 12分
. 12分解法二:以O为坐标原点,OB,OC,OA
 所在直线分别为x轴,y轴,z轴建立空间直角坐标系, 7分
所在直线分别为x轴,y轴,z轴建立空间直角坐标系, 7分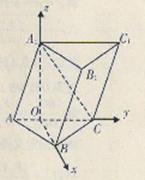
则A(0,-2,0),B(2
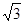 ,0,0),C(0,2,0),A
,0,0),C(0,2,0),A (0,0,2),
(0,0,2),C
 (0,4,2),设n=(x,y,z)是面A
(0,4,2),设n=(x,y,z)是面A ABB
ABB 的一个法向量,则n⊥
的一个法向量,则n⊥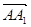 ,n⊥
,n⊥ ,
,∵
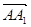 =(0,2,2),
=(0,2,2),  =(2
=(2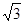 ,2,0), 8分
,2,0), 8分∴
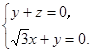 取x=1,得n=(1,-
取x=1,得n=(1,-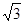 ,
,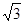 ). 9分
). 9分易知平面ABC的法向量为m=(0,0,1), 10分
所以cos<m,n>=
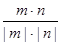 =
=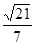 . 11分
. 11分∴ 侧面A
 ABB
ABB 与底面ABC所成的二面角为arccos
与底面ABC所成的二面角为arccos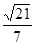 . 12分
. 12分点评:主要是考查了关于垂直证明,以及二面角的平面角的求解,属于基础题。可以运用代数法也可以运用几何性质来求解和证明。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






 的主视图(又称正视图)是边长为4的正方形, 则此正三棱柱的侧视图(又称左视图)的面积为( )
的主视图(又称正视图)是边长为4的正方形, 则此正三棱柱的侧视图(又称左视图)的面积为( )




 为正三角形,
为正三角形, ,
, ,且
,且

 ,则多面体
,则多面体 的正视图(也称主视图)是( )
的正视图(也称主视图)是( )
 ;
;