题目内容

设集合A=[0，），B=[，1]，函数f （x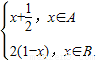）=若x∈A，且f[f （x）]∈A，则x的取值范围是（ ）
A．（0，]
B．[，]
C．（，）
D．[0，]
【答案】分析：利用当 x∈A时，f[f （x）]∈A，列出不等式，解出 x的取值范围．
解答：解：∵0≤x＜，∴f（x）=x0 +∈[，1]⊆B，
∴f[f（x）]=2（1-f（x））=2[1-（x+）]=2（-x）．
∵f[f（x）]∈A，∴0≤2（-x）＜，∴＜x≤．
又∵0≤x＜，∴＜x＜． 
故选C．
点评：本题考查求函数值的方法，以及不等式的解法，属于基础题．
练习册系列答案
相关题目
设集合A=[0，
1
2
），B=[
1
2
，1]，函数f （x）=
x+
1
2
，x∈A
2(1-x)，x∈B
，若x0∈A，且f[f （x0）]∈A，则x0的取值范围是（　　）
A、（0，
1
4
]
B、[
1
4
，
1
2
]
C、（
1
4
，
1
2
）
D、[0，
3
8
]
设集合A={0，2，4，6}，B={1，3，5，7}，从集合A，B中各取2个元素组成没有重复数字的四位数．
（1）可组成多少个这样的四位数？
（2）有多少个是2的倍数或是5的倍数？
（2007•惠州模拟）设n为正整数，规定：fn(x)=
f{f[…f(x)]}
n个f
，已知f(x)=
2(1-x)，0≤x≤1
x-1，1＜x≤2
，
（1）解不等式f（x）≤x；
（2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
（3）求f2007(
8
9
)的值；
（4）若集合B={x|f12（x）=x，x∈[0，2]}，证明：B中至少包含8个元素．
设n为正整数，规定：fn(x)=
f{f[…f(x)…]}
n个f
，已知f(x)=
2(1-x)
x-1
，
，
(0≤x≤1)
(1＜x≤2)
．
（1）解不等式：f（x）≤x；
（2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
（3）探求f2009(
8
9
)；
（4）若集合B={x|f12（x）=x，x∈[0，2]}，证明：B中至少包含有8个元素．
已知n为正整数，规定f1（x）=f（x），fn+1（x）=f（fn（x）），已知f(x)=
2(1-x)，0≤x≤1
x-1，
 1＜x≤2
，
（1）解不等式f（x）≤x；
（2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网