题目内容
 如图,F1、F2是椭圆
如图,F1、F2是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| OM |
| ||
| 2 |
| OF2 |
| AF1 |
| AF2 |
(1)求椭圆的离心率;(2)若△ABF1的周长为4
| 6 |
分析:(1)设出F1(-c,0),F2(c,0),A(x0,y0),利用椭圆的离心率为e,推断出|AF1|=a+ex0、|AF2|=a-ex0得
•
=0,进而利用a,b和c的关系求得a和c的关系及椭圆的离心率.
(2)根据题意,△ABF2的周长为4
,即BF2+AF2+BF1+AF1=4
,结合椭圆的定义,即可得a的值;又由椭圆的离心率,可得c的值,进而可得b的值;由椭圆的焦点在x轴上,可得椭圆的方程.
| AF1 |
| AF2 |
(2)根据题意,△ABF2的周长为4
| 6 |
| 6 |
解答:解:(1)设F1(-c,0),F2(c,0),A(x0,y0),椭圆的离心率为e,则M(
c,0),x0=
c.
∵
=e,∴|AF1|=a+ex0.…(2分)
同理|AF2|=a-ex0.…(3分)
∵
•
=0,∴AF1⊥AF2,∴|AF1|2+|AF2|2=|F1F2|2,
∴(a+ex0)2+(a-ex0)2=4c2即a2+e2x02=2c2.
∵x0=
c,∴a2+e2•
c2=2c2,…(5分)
∴1+
e4=2e2,即3e4-8e2+4=0,…(7分)
∴e2=
或e2=2(舍去)…(9分)
所以椭圆的离心率e=
.…(10分)
(2)∵△ABF2的周长为4
,∴4a=4
,a=
…(12分)
又∵
=
∴c=2,….(13分)
∴b2=2.∴椭圆的方程为
+
=1….(15分)
| ||
| 2 |
| ||
| 2 |
∵
| |AF1| | ||
x0+
|
同理|AF2|=a-ex0.…(3分)
∵
| AF1 |
| AF2 |
∴(a+ex0)2+(a-ex0)2=4c2即a2+e2x02=2c2.
∵x0=
| ||
| 2 |
| 3 |
| 4 |
∴1+
| 3 |
| 4 |
∴e2=
| 2 |
| 3 |
所以椭圆的离心率e=
| ||
| 3 |
(2)∵△ABF2的周长为4
| 6 |
| 6 |
| 6 |
又∵
| c |
| a |
| ||
| 3 |
∴b2=2.∴椭圆的方程为
| x2 |
| 6 |
| y2 |
| 2 |
点评:本题考查椭圆的性质,此类题型一般与焦点三角形联系,难度一般不大;注意结合椭圆的基本几何性质解题,注意利用题设中a,b和c的关系.

练习册系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C: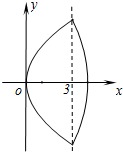 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: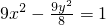 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;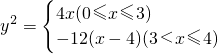 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;  )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: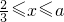 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.