题目内容
 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| x0 |
| a |
| y0 |
| b |
(1)求椭圆C的标准方程;
(2)△AOB的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
分析:(1)由离心率e=
,S△DEF2=1-
,可得
=
,
(a-c)b=1-
,又a2=b2+c2.联立解得即可.
(2)设A(x1,y1),B(x2,y2),则P(
,y1),Q(
,y2).由
⊥
,可得
•
=
+y1y2=0.(*)设直线l的方程为my+t=x,与椭圆方程联立可得根与系数的关系,代入(*)可得m,t的关系,利用两点间的距离公式可得|AB|,利用点的直线距离公式可得点O到直线AB的距离,利用三角形的面积计算公式即可得出定值.
| ||
| 2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(2)设A(x1,y1),B(x2,y2),则P(
| x1 |
| 2 |
| x2 |
| 2 |
| OP |
| OQ |
| OP |
| OQ |
| x1x2 |
| 4 |
解答:解:(1)∵椭圆C:
+
=1(a>b>0)的离心率e=
,S△DEF2=1-
,
∴
=
①,
(a-c)b=1-
②,又a2=b2+c2③.
由①②③组成方程组,解得a2=4,b2=1.
∴椭圆C的标准方程为
+y2=1.
(2)设A(x1,y1),B(x2,y2),则P(
,y1),Q(
,y2).
∵
⊥
,∴
•
=
+y1y2=0.(*)
设直线l的方程为my+t=x,联立
,化为(4+m2)y2+2mty+t2-4=0,
∵直线l与椭圆相交于两点,∴△=4m2t2-4(4+m2)(t2-4)>0,化为m2+4>t2.(**)
∴y1+y2=-
,y1y2=
,
∴x1x2=(my1+t)(my2+t)=m2y1y2+mt(y1+y2)+t2,
代入(*)可得(m2+4)y1y2+mt(y1+y2)+t2=0.
∴t2-4-
+t2=0,
∴t2=
,代入(**)知成立.
|AB|=
=
=
.
点O到直线AB的距离d=
.
又S△AOB=
|AB|•d=2为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由①②③组成方程组,解得a2=4,b2=1.
∴椭圆C的标准方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),则P(
| x1 |
| 2 |
| x2 |
| 2 |
∵
| OP |
| OQ |
| OP |
| OQ |
| x1x2 |
| 4 |
设直线l的方程为my+t=x,联立
|
∵直线l与椭圆相交于两点,∴△=4m2t2-4(4+m2)(t2-4)>0,化为m2+4>t2.(**)
∴y1+y2=-
| 2mt |
| 4+m2 |
| t2-4 |
| 4+m2 |
∴x1x2=(my1+t)(my2+t)=m2y1y2+mt(y1+y2)+t2,
代入(*)可得(m2+4)y1y2+mt(y1+y2)+t2=0.
∴t2-4-
| 2m2t2 |
| 4+m2 |
∴t2=
| 4+m2 |
| 2 |
|AB|=
| (1+m2)[(y1+y2)2-4y1y2] |
(1+m2)[
|
4
| ||
| 4+m2 |
点O到直线AB的距离d=
| |t| | ||
|
又S△AOB=
| 1 |
| 2 |
点评:本题考查了直线与椭圆相交问题转化为方程联立可得根与系数的关系、两点间的距离公式、点的直线距离公式、三角形的面积计算公式、新定义、向量垂直与数量积的关系等基础知识与基本技能方法,考查了推理能力和计算能力,考查了分析问题和解决问题的能力,属于难题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: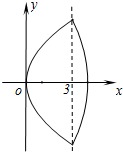 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: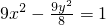 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;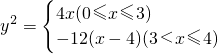 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 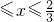 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: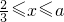 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.