题目内容
在△ABC中,设向量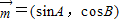 ,
,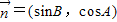 且
且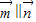 ,
, .
.(1)求证:A+B=
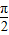 ;
;(2)求sinA+sinB的取值范围;
(3)若(sinAsinB)x=sinA+sinB,试确定实数x的取值范围.
【答案】分析:(1)由题意可得sin2A=sin2B,进而可得A=B,或A+B=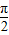 ,经验证可排除A=B;
,经验证可排除A=B;
(2)可得sinA+sinB=sinA+sin(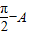 )=
)= sin(A+
sin(A+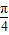 ),由A的范围逐步可得;
),由A的范围逐步可得;
(3)可得x=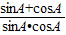 ,令sinA+cosA=t∈(1,
,令sinA+cosA=t∈(1,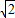 ],换元后可得关于t的函数,由t的范围可得.
],换元后可得关于t的函数,由t的范围可得.
解答:解:(1)∵向量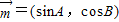 ,
,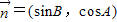 且
且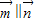 ,
,
∴sinAcosA-sinBcosB=0,即sin2A=sin2B,解得2A=2B或2A+2B=π,
化简可得A=B,或A+B=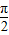 ,但A=B时有
,但A=B时有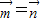 ,与已知矛盾,故舍去,
,与已知矛盾,故舍去,
故有A+B=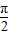 ;
;
(2)由(1)可知A+B=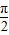 ,故sinA+sinB=sinA+sin(
,故sinA+sinB=sinA+sin(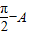 )
)
=sinA+cosA=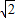 sin(A+
sin(A+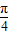 ),
),
∵0<A<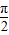 ,∴
,∴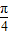 <A+
<A+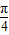 <
<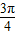 ,∴1<
,∴1<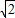 sin(A+
sin(A+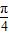 )≤
)≤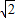
故sinA+sinB的取值范围是(1,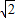 ];
];
(3)由题意可知x=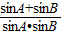 =
=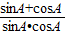 ,
,
设sinA+cosA=t∈(1,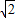 ],则t2=1+2sinAcosA,故sinAcosA=
],则t2=1+2sinAcosA,故sinAcosA=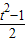 ,
,
代入可得x= =
=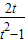 =
=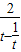 ≥
≥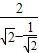 =2
=2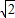
故实数x的取值范围为:[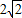 ,+∞)
,+∞)
点评:本题考查向量的平行和共线,涉及三角函数的运算,属基础题.
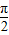 ,经验证可排除A=B;
,经验证可排除A=B;(2)可得sinA+sinB=sinA+sin(
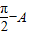 )=
)= sin(A+
sin(A+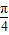 ),由A的范围逐步可得;
),由A的范围逐步可得;(3)可得x=
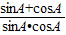 ,令sinA+cosA=t∈(1,
,令sinA+cosA=t∈(1,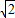 ],换元后可得关于t的函数,由t的范围可得.
],换元后可得关于t的函数,由t的范围可得.解答:解:(1)∵向量
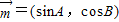 ,
,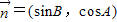 且
且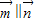 ,
,∴sinAcosA-sinBcosB=0,即sin2A=sin2B,解得2A=2B或2A+2B=π,
化简可得A=B,或A+B=
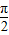 ,但A=B时有
,但A=B时有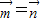 ,与已知矛盾,故舍去,
,与已知矛盾,故舍去,故有A+B=
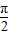 ;
;(2)由(1)可知A+B=
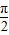 ,故sinA+sinB=sinA+sin(
,故sinA+sinB=sinA+sin(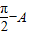 )
)=sinA+cosA=
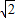 sin(A+
sin(A+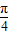 ),
),∵0<A<
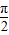 ,∴
,∴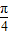 <A+
<A+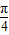 <
<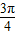 ,∴1<
,∴1<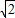 sin(A+
sin(A+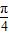 )≤
)≤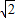
故sinA+sinB的取值范围是(1,
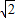 ];
];(3)由题意可知x=
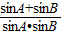 =
=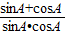 ,
,设sinA+cosA=t∈(1,
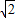 ],则t2=1+2sinAcosA,故sinAcosA=
],则t2=1+2sinAcosA,故sinAcosA=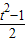 ,
,代入可得x=
 =
=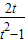 =
=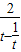 ≥
≥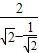 =2
=2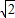
故实数x的取值范围为:[
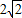 ,+∞)
,+∞)点评:本题考查向量的平行和共线,涉及三角函数的运算,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,求证:△ABC的面积
,求证:△ABC的面积 .
.
 ,
, .
. .
.