题目内容
设[x]表示不超过实数x的最大整数,如[0.3]=0,[-0.4]=-1.则在坐标平面内满足方程[x]2+[y]2=25的点(x,y)所构成的图形的面积为
- A.8
- B.10
- C.12
- D.14
C
分析:根据方程可得对于x,y≥0时,求出x,y的整数解,可得|[x]|可能取的数值为5、4、3、0,则可以确定x的范围,进而得到对应的y的范围,求出面积即可.
解答:由题意可得:方程:[x]2+[y]2=25
当x,y≥0时,[x],[y]的整解有两组,(3,4),(0,5),所以此时x可能取的数值为:5,4,3,0.
所以当|[x]|=5时,5≤x<6,或者-5≤x<-4,|[y]|=0,0≤y<1,围成的区域是2个单位正方形
当|[x]|=4时,4≤x<5,或者-4≤x<-3,|[y]|=3,-3≤y<-2,或者3<y≤4,围成的区域是4个单位正方形
当|[x]|=3时,3≤x<4,或者-3≤x<-2,|[y]|=4,-4≤y<-3,或者4<y≤5,围成的区域是4个单位正方形
当|[x]|=0时,0≤x<1,|[y]|=5,5≤y<6 或者-5≤y<-4,围成的区域是2个单位正方形
所以总面积是:12
故选C.
点评:本题考查探究性问题,是创新题,考查学生分析问题,解决问题的能力,而分类讨论思想是高中数学的一个重要的数学思想,高考中经常涉及.
分析:根据方程可得对于x,y≥0时,求出x,y的整数解,可得|[x]|可能取的数值为5、4、3、0,则可以确定x的范围,进而得到对应的y的范围,求出面积即可.
解答:由题意可得:方程:[x]2+[y]2=25
当x,y≥0时,[x],[y]的整解有两组,(3,4),(0,5),所以此时x可能取的数值为:5,4,3,0.
所以当|[x]|=5时,5≤x<6,或者-5≤x<-4,|[y]|=0,0≤y<1,围成的区域是2个单位正方形
当|[x]|=4时,4≤x<5,或者-4≤x<-3,|[y]|=3,-3≤y<-2,或者3<y≤4,围成的区域是4个单位正方形
当|[x]|=3时,3≤x<4,或者-3≤x<-2,|[y]|=4,-4≤y<-3,或者4<y≤5,围成的区域是4个单位正方形
当|[x]|=0时,0≤x<1,|[y]|=5,5≤y<6 或者-5≤y<-4,围成的区域是2个单位正方形
所以总面积是:12
故选C.
点评:本题考查探究性问题,是创新题,考查学生分析问题,解决问题的能力,而分类讨论思想是高中数学的一个重要的数学思想,高考中经常涉及.

练习册系列答案
相关题目
设函数f(x)=
(a>0,且a≠1),[m]表示不超过实数m的最大整数,则实数[f(x)-
]+[f(-x)-
]的值域是
( )
| ax |
| 1+ax |
| 1 |
| 2 |
| 1 |
| 2 |
( )
| A、[-1,1] |
| B、[0,1] |
| C、{-1,0} |
| D、{-1,1} |
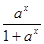 (a>0,且a≠1),〔m〕表示不超过实数m的最大整数,则
(a>0,且a≠1),〔m〕表示不超过实数m的最大整数,则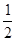 〕+〔f(-x)-
〕+〔f(-x)- (
( >0,
且
>0,
且 1),[m]表示不超过实数m的最大整数,则函数[f(x)
1),[m]表示不超过实数m的最大整数,则函数[f(x) ]+[f
]+[f ]的值域是( )
]的值域是( )