题目内容
若数列{an}的首项为a1=1,且对任意n∈N*,an与an+1恰为方程x2-bnx+cn=0的两根,其中0<|c|<1,当 (b1+b2+…+bn)≤3,求c的取值范围.
(b1+b2+…+bn)≤3,求c的取值范围.
解:∵对任意n∈N*,an与an+1恰为方程x2-bnx+cn=0的两根,
∴an+an+1=bn,an•an+1=cn
∴ =
=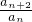 =
= =c.
=c.
∵a1=1,∴a1•a2=a2=c.
∴a1,a3,a5,…,a2n-1,构成首项为1,公比为c的等比数列,
a2,a4,a6,…,a2n,构成首项为c,公比为c的等比数列.
又∵任意n∈N*,an+an+1=bn恒成立.
∴ =
= =c.又b1=a1+a2=1+c,b2=a2+a3=2c,
=c.又b1=a1+a2=1+c,b2=a2+a3=2c,
∴b1,b3,b5,…,b2n-1,构成首项为1+c,公比为c的等比数列,
b2,b4,b6,…,b2n,构成首项为2c,公比为c的等比数列,
∵0<|c|<1, cn=0
cn=0
∴ (b1+b2+b3+…+bn)=
(b1+b2+b3+…+bn)= (b1+b3+b5+…)+
(b1+b3+b5+…)+ (b2+b4+…)
(b2+b4+…)
= +
+ ≤3.
≤3.
解得c≤ 或c>1.
或c>1.
∵0<|c|<1,∴0<c≤ 或-1<c<0.
或-1<c<0.
故c的取值范围是(-1,0)∪(0, ].
].
分析:由题意再根据韦达定理列出an,an+1和bn三者的关系式,再进行变形求出数列{an}和{bn}的特点,对数列分组求和,再由0<|c|<1求极限不等式,最后求出c的值.
点评:本题综合性强,涉及的知识面广.本题的关键在于根据韦达定理求出数列{an}和{bn}的特点,进行数列分组求和,将题设中的极限不等式转化为关于c的不等式,显然“桥梁”应是一元二次方程根与系数的关系.
∴an+an+1=bn,an•an+1=cn
∴
 =
=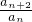 =
= =c.
=c.∵a1=1,∴a1•a2=a2=c.
∴a1,a3,a5,…,a2n-1,构成首项为1,公比为c的等比数列,
a2,a4,a6,…,a2n,构成首项为c,公比为c的等比数列.
又∵任意n∈N*,an+an+1=bn恒成立.
∴
 =
= =c.又b1=a1+a2=1+c,b2=a2+a3=2c,
=c.又b1=a1+a2=1+c,b2=a2+a3=2c,∴b1,b3,b5,…,b2n-1,构成首项为1+c,公比为c的等比数列,
b2,b4,b6,…,b2n,构成首项为2c,公比为c的等比数列,
∵0<|c|<1,
 cn=0
cn=0∴
 (b1+b2+b3+…+bn)=
(b1+b2+b3+…+bn)= (b1+b3+b5+…)+
(b1+b3+b5+…)+ (b2+b4+…)
(b2+b4+…)=
 +
+ ≤3.
≤3.解得c≤
 或c>1.
或c>1.∵0<|c|<1,∴0<c≤
 或-1<c<0.
或-1<c<0.故c的取值范围是(-1,0)∪(0,
 ].
].分析:由题意再根据韦达定理列出an,an+1和bn三者的关系式,再进行变形求出数列{an}和{bn}的特点,对数列分组求和,再由0<|c|<1求极限不等式,最后求出c的值.
点评:本题综合性强,涉及的知识面广.本题的关键在于根据韦达定理求出数列{an}和{bn}的特点,进行数列分组求和,将题设中的极限不等式转化为关于c的不等式,显然“桥梁”应是一元二次方程根与系数的关系.

练习册系列答案
相关题目