题目内容
已知两定点A(2,5),B(-2,1),M和N是过原点的直线l上的两个动点,且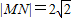 ,l∥AB,如果直线AM和BN的交点C在y轴上;
,l∥AB,如果直线AM和BN的交点C在y轴上;(Ⅰ)求M,N与C点的坐标;
(Ⅱ)求C点到直线l的距离.
【答案】分析:(Ⅰ) 用点斜式求出直线l 的方程,设M(a,a),则N(a+2,a+2),设C(0,b),根据点共线得到①和②,
解得 a 和 b 的值,即得M,N与C点的坐标.
(Ⅱ)由两点式求得AB的方程,由点到直线的距离公式求得C点到直线l的距离.
解答:解:(Ⅰ) 直线l的斜率即AB的斜率,为 =1,故过原点的直线l 的方程为 y=x.
=1,故过原点的直线l 的方程为 y=x.
设M(a,a),则N(a+2,a+2),设C(0,b),由A、C、M三点共线可得 =
= ①.
①.
由B、C、N 三点共线可得 =
= ②.
②.
由①②解得 a=-1,b=1,∴M(-1,-1),N(1,1),C (0,1).
(Ⅱ)由两点式求得AB的方程为 ,即 x-y+3=0,故C点到直线l的距离为
,即 x-y+3=0,故C点到直线l的距离为
 =
= .
.
点评:本题考查用点斜式、两点式求直线方程,三点共线的性质,点到直线的距离公式,求出点C的坐标,是解题的关键.
解得 a 和 b 的值,即得M,N与C点的坐标.
(Ⅱ)由两点式求得AB的方程,由点到直线的距离公式求得C点到直线l的距离.
解答:解:(Ⅰ) 直线l的斜率即AB的斜率,为
 =1,故过原点的直线l 的方程为 y=x.
=1,故过原点的直线l 的方程为 y=x.设M(a,a),则N(a+2,a+2),设C(0,b),由A、C、M三点共线可得
 =
= ①.
①.由B、C、N 三点共线可得
 =
= ②.
②. 由①②解得 a=-1,b=1,∴M(-1,-1),N(1,1),C (0,1).
(Ⅱ)由两点式求得AB的方程为
 ,即 x-y+3=0,故C点到直线l的距离为
,即 x-y+3=0,故C点到直线l的距离为  =
= .
.点评:本题考查用点斜式、两点式求直线方程,三点共线的性质,点到直线的距离公式,求出点C的坐标,是解题的关键.

练习册系列答案
相关题目
已知两定点A(-3,5),B(2,15),动点P在直线3x-4y+4=0上,则|PA|+|PB|的最小值为( )
A、5
| ||
B、
| ||
C、15
| ||
D、5+10
|
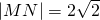 ,l∥AB,如果直线AM和BN的交点C在y轴上;
,l∥AB,如果直线AM和BN的交点C在y轴上;