题目内容
已知两定点A(2,5),B(-2,1),直线l过原点,且l∥AB,点M(在第一象限)和点N都在l上,且|MN|=2
,如果AM和BN的交点C在y轴上,求点C的坐标.
| 2 |
分析:利用斜率计算公式和平行线的性质即可得出直线l的方程,再利用三角形的中位线定理和中点坐标公式即可得出.
解答:解:∵kAB=
=1,l∥AB,∴kl=1,
∴直线l的方程为y=x.
∵线段AB的中点为P(0,3),线段MN的中点为原点O(0,0).
∴|OM|=
.
设M(x,x)(x>0),则
=
,解得x=1,
∴M(1,1),点M为线段AC的中点,
∴1=
,解得yC=-3.
∴C(0,-3).
| 1-5 |
| -2-2 |
∴直线l的方程为y=x.
∵线段AB的中点为P(0,3),线段MN的中点为原点O(0,0).
∴|OM|=
| 2 |
设M(x,x)(x>0),则
| 2x2 |
| 2 |
∴M(1,1),点M为线段AC的中点,
∴1=
| 5+yC |
| 2 |
∴C(0,-3).
点评:熟练掌握斜率计算公式和平行线的性质、三角形的中位线定理和中点坐标公式等是解题的关键.

练习册系列答案
相关题目
已知两定点A(-3,5),B(2,15),动点P在直线3x-4y+4=0上,则|PA|+|PB|的最小值为( )
A、5
| ||
B、
| ||
C、15
| ||
D、5+10
|
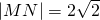 ,l∥AB,如果直线AM和BN的交点C在y轴上;
,l∥AB,如果直线AM和BN的交点C在y轴上;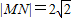 ,l∥AB,如果直线AM和BN的交点C在y轴上;
,l∥AB,如果直线AM和BN的交点C在y轴上;