题目内容
已知点A,B分别是射线l1:y=x(x≥0),l2:y=-x(x≥0)上的动点,O为坐标原点,且△OAB的面积为定值2.(1)求线段AB中点M的轨迹C的方程;
(2)过点N(0,2)作直线l,与曲线C交于不同的两点P,Q,与射线l1,l2分别交于点R,S,若点P,Q恰为线段RS的两个三等分点,求此时直线l的方程.
解:(1)由题意可设A(x1,x1),B(x2,-x2),M(x,y),其中x1>0,x2>0,
则 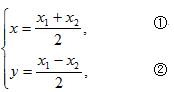
∵△OAB的面积为定值2,
∴S△OAB=![]() |OA|·|OB|=
|OA|·|OB|=![]() (
(![]() x1)(
x1)(![]() x2)=x1x2=2.
x2)=x1x2=2.
①2-②2,消去x1,x2,得x2-y2=2.
由于x1>0,x2>0,∴x>0.
∴点M的轨迹方程为x2-y2=2(x>0).
(2)依题意,直线l的斜率存在,设直线l的方程为y=kx+2.
由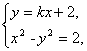 消去y得(1-k2)x2-4kx-6=0,
消去y得(1-k2)x2-4kx-6=0,
设点P、Q、R、S的横坐标分别是xP、xQ、xR、xS,
∴由xP,xQ>0得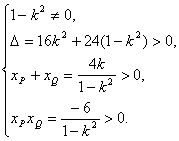 0.
0.
解之,得-![]() <k<-1.
<k<-1.
∴|xP-xQ|=![]() .
.
由![]() 消去y,得xR=
消去y,得xR=![]() ,
,
由![]() 消去y,得xS=
消去y,得xS=![]() ,
,
∴|xR-xS|=![]() .
.
由于P,Q为RS的三等分点,∴|xR-xS|=3|xP-xQ|.
解之,得k=![]() .
.
经检验,此时P,Q恰为RS的三等分点,故所求直线方程为y=![]() x+2.
x+2.

练习册系列答案
相关题目
 (x-4),则这条直线经过的已知点,倾斜角分别是
(x-4),则这条直线经过的已知点,倾斜角分别是 的坐标分别是
的坐标分别是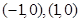 ,直线
,直线 相交于点
相交于点 ,
且直线
,
且直线 与直线
与直线 的斜率之差是
的斜率之差是 ,则点
,则点 B.
B. C.
C. D.
D.