Question

已知F₁、F₂分别是双曲线L：

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左、右焦点，过点F₁作斜率为2的直线l交双曲线L的左支上方于点P，若∠F₁PF₂为直角，则此双曲线的离心率等于

5

．

Answer 1

分析：先得出过点F₁且斜率为2的直线l的方程，再利用垂直关系得出直线PF₁的方程，求出它们的交点坐标即为P的坐标，利用P在双曲线上，其坐标适合方程，将点的坐标代入双曲线方程得出关于a，b，c的关系式，最后把等量关系转化为用a，c来表示即可求双曲线C的离心率．

解答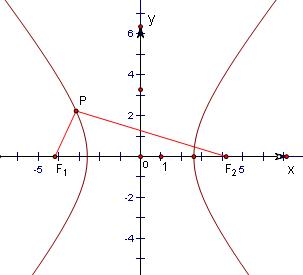：解：由题意得，过点F₁作斜率为2的直线l为y=2（x+c），
又因∠F₁PF₁为直角，∴直线PF₁的斜率为-

1

2

，直线PF₁的方程为：y=-

1

2

（x-c），
两直线联立，解得交点P的坐标为（-

3c

5

，

4c

5

），如图．
将P的坐标代入双曲线方程，得

(- 3c 5 )2

a2

-

( 4c 5 )2

b2

=1，
即9b²c²-16a²c²=25a²b²，又b²=c²-a²，
代入得：9（c²-a²）c²-16a²c²=25a²（c²-a²）．
化简得：9c⁴-50a²c²+25a⁴=0．
解得

c

a

=

5

．
故答案为：

5

．

点评：本题是对双曲线性质中离心率的考查．求离心率，只要找到a，c之间的等量关系即可求．是基础题．