题目内容
9．
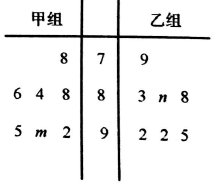某中学奥数培训班共有14人，分为两个小组，在一次阶段测试中两个小组成绩的茎叶图如图所示，其中甲组学生成绩的平均数是88，乙组学生成绩的中位数是89，则n-m的值（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 利用茎叶图、平均数、中位数的性质，列出方程组，求出m，n，由此能求出结果．
解答 解：由题意得：
$\left\{\begin{array}{l}{\frac{1}{7}（78+88+84+86+92+90+m+95）=88}\\{\80+n=89}\end{array}\right.$，
解得m=3，n=9，
∴n-m=9-3=6．
故选：B．
点评 本题考查代数式求和，是基础题，解题时要认真审题，注意茎叶图的性质的合理运用．
练习册系列答案
相关题目
19．已知命题p：?x∈R，2x=5，则￢p为（ ）
| A． | ?x∉R，2x≠5 | B． | ?x∈R，2x≠5 | C． | ?x∉R，2x≠5 | D． | ?x∈R，2x≠5 |
4．下列四组函数中表示同一函数的是（ ）
| A． | f（x）=$\root{3}{{x}^{3}}$与$g（x）=\sqrt{x^2}$ | B． | f（x）=|x|与$g（x）={（{\sqrt{x}}）^2}$ | ||
| C． | $f（x）=\sqrt{1-x}×\sqrt{1+x}$与$g（x）=\sqrt{1-{x^2}}$ | D． | f（x）=x0与g（x）=1 |
14．已知抛物线y2=2x上一点A到焦点F距离与其到对称轴的距离之比为5：4，且|AF|＞2，则A点到原点的距离为（ ）
| A． | $\sqrt{41}$ | B． | 2$\sqrt{2}$ | C． | 4 | D． | 8 |
1．已知$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，且$\overrightarrow{a}⊥\overrightarrow{b}$，向量$\overrightarrow{c}$满足|$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=2，则|$\overrightarrow{c}$|的范围为（ ）
| A． | [1，1+$\sqrt{2}$] | B． | [2-$\sqrt{2}$，2+$\sqrt{2}$] | C． | [$\sqrt{2}，2\sqrt{2}$] | D． | [3-2$\sqrt{2}$，3+2$\sqrt{2}$] |