题目内容
17．
如图，在边长为1的正方形中随机撒1000粒豆子，有380粒落到阴影部分，据此估计阴影部分的面积为0.38．
分析 根据几何槪型的概率意义，即可得到结论．
解答 解：正方形的面积S=1，设阴影部分的面积为S，
∵随机撒1000粒豆子，有380粒落到阴影部分，
∴由几何槪型的概率公式进行估计得$\frac{S}{1}=\frac{380}{1000}$，
即S=0.38，
故答案为：0.38．
点评 本题主要考查几何槪型的概率的计算，利用豆子之间的关系建立比例关系是解决本题的关键，比较基础．
练习册系列答案
相关题目
2．如图所示，双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，M，N为双曲线C上两点，且kMN=0，若$\overrightarrow{{F}_{1}Q}$=$\overrightarrow{QN}$（Q在双曲线C上），且|MN|=$\frac{{|F}_{1}{F}_{2}|}{4}$，则双曲线C的渐近线方程为（ ）
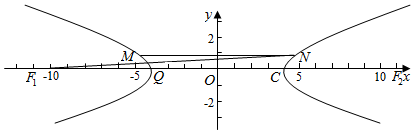
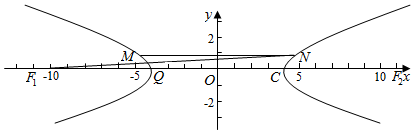
| A． | y=$±\sqrt{2}$x | B． | y=$±\sqrt{3}$x | C． | y=±2x | D． | y=$±\sqrt{5}$x |