题目内容
设
，
是两个非零向量，如果（
+3
）⊥（7
-5
），且（
-4
）⊥（7
-2
），则
与
的夹角为
．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| π |
| 3 |
分析：由已知可得：7
2+16
•
-15
2=0，并且 7
2-30
•
+8
2=0，整理可得
2=-2
•
，将
2=-2
•
代回原式可得
2=-2
•
，即可得到
2 =
2，即|
|=|
|，再
根据向量的夹角公式可求答案．
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
根据向量的夹角公式可求答案．
解答：解：因为 (
+3
)⊥(7
-5
)，
所以 7
2+16
•
-15
2=0，
因为 (
-4
)⊥(7
-2
)，
所以 7
2-30
•
+8
2=0，
两式相减得 46
•
-23
2=0，
所以
2=2
•
，
将
2=2
•
代回第一个式子可得：
2=2
•
，
所以
2 =
2，即|
|=|
|．
设向量
与
的夹角为θ，则 cosθ=
=
，
所以向量
与
的夹角大小为
．
故答案为：
．
| a |
| b |
| a |
| b |
所以 7
| a |
| a |
| b |
| b |
因为 (
| a |
| b |
| a |
| b |
所以 7
| a |
| a |
| b |
| b |
两式相减得 46
| a |
| b |
| b |
所以
| b |
| a |
| b |
将
| b |
| a |
| b |
| a |
| a |
| b |
所以
| a |
| b |
| a |
| b |
设向量
| a |
| b |
| ||||
|
|
| 1 |
| 2 |
所以向量
| a |
| b |
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题主要考查了平面向量的数量积的性质：若
⊥
?
•
=0的应用，即若知道向量垂直，则可得向量的数量积为0．
| a |
| b |
| a |
| b |
练习册系列答案
备战中考寒假系列答案
相关题目
，
是两个非零向量，则“向量
，
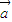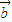是两个非零向量，则“向量
，
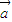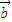的夹角为锐角”是“函数f（x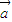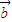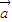）=（x
+
）•（
-x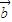
）的图象是一条开口向下的抛物线”的（ ）