题目内容
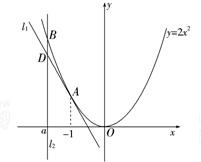 已知A(-1,2)为抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a<-1)交抛物线C于点B,交直线l1于点D.
已知A(-1,2)为抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a<-1)交抛物线C于点B,交直线l1于点D.(1)求直线l1的方程;
(2)求△ABD的面积S1.
分析:(1)先对函数y=2x2进行求导,得到直线l1的斜率,再由点斜式方程得到直线l1的方程.
(2)联立直线l2、l1与抛物线方程可求得B,D的坐标,进而得到|BD|的值,即根据三角形面积公式可求出△ABD的面积S1.
(2)联立直线l2、l1与抛物线方程可求得B,D的坐标,进而得到|BD|的值,即根据三角形面积公式可求出△ABD的面积S1.
解答:解:(1)对y=2x2进行求导得到y'=4x
∴k=4×(-1)=-4
直线l1的方程为(y-2)=-4(x+1),即:y=-4x-2.
(2)联立直线l2、直线l1与抛物线方程得到B为(a,2a2),D(a,-4a-2 )
∴|BD|=|2a2+4a+2|=2(a+1)2
∴S1=
×2(a+1)2×|(a+1)|=|a+1|3
∴k=4×(-1)=-4
直线l1的方程为(y-2)=-4(x+1),即:y=-4x-2.
(2)联立直线l2、直线l1与抛物线方程得到B为(a,2a2),D(a,-4a-2 )
∴|BD|=|2a2+4a+2|=2(a+1)2
∴S1=
| 1 |
| 2 |
点评:本题主要考查导数的几何意义和直线与抛物线的综合题.考查基础知识的综合应用.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知A(1,2)为椭圆
+
=1内一点,则以A为中点的椭圆的弦所在的直线方程为( )
| x2 |
| 4 |
| y2 |
| 16 |
| A、x+2y+4=0 |
| B、x+2y-4=0 |
| C、2x+y+4=0 |
| D、2x+y-4=0 |
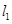 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线 :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线
 的面积为S1,求
的面积为S1,求 及S1的值.
及S1的值. 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.