题目内容

已知A（1，2）为椭圆
x2
4
+
y2
16
=1内一点，则以A为中点的椭圆的弦所在的直线方程为（　　）
A、x+2y+4=0
B、x+2y-4=0
C、2x+y+4=0
D、2x+y-4=0
分析：首先根据题意设出直线的方程，再联立直线与椭圆的方程，然后结合题意与跟与系数的关系得到答案．
解答：解：设直线的方程为y-2=k（x-1），
联立直线与椭圆的方程代入可得：（4+k2）x2+2k（2-k）x+k2-4k-12=0
因为A为椭圆的弦的中点，
所以
2k(k-2)
4+k2
=2，解得k=-2，
所以直线的方程为2x+y-4=0．
故选D．
点评：解决此类问题的关键是熟练掌握直线与椭圆的位置关系的判定，以及掌握弦中点与中点弦问题．
练习册系列答案
相关题目
精英家教网
如图，四边形OABC为矩形，点A、C的坐标分别为（a+1，0）（a＞1）、（0，1），点D在OA上，坐标为（a，0），椭圆C分别以OD、OC为长、短半轴，CD是椭圆在矩形内部的椭圆弧．已知直线l：y=-x+m与椭圆弧相切，且与AD相交于点E．
（Ⅰ）当m=2时，求椭圆C的标准方程；
（Ⅱ）圆M在矩形内部，且与l和线段EA都相切，若直线l将矩形OABC分成面积相等的两部分，求圆M面积的最大值．
如图，F1，F2为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，D，E是椭圆的两个顶点，椭圆的离心率e=
3
2
，S△DEF2=1-
3
2
．若点M（x0，y0）在椭圆C上，则点N（
x0
a
，
y0
b
）称为点M的一个“椭点”．直线l与椭圆交于A，B两点，A，B两点的“椭点”分别为P，Q，已知以PQ为直径的圆经过坐标原点O．
（1）求椭圆C的标准方程；
（2）△AOB的面积是否为定值？若为定值，试求出该定值；若不为定值，请说明理由．
（2012•淮南二模）已知椭圆C：
x2
a2
+
y2
b2
=1，（a＞b＞0）与双曲4x2-
4
3
y2=1有相同的焦点，且椭C的离心e=
1
2
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
（1）求椭圆的方程；
（2）若直MA交直x=4于点P，过P作直线MB的垂线x轴于点Q，Q的坐标；
（3）求点P在直线MB上射R的轨迹方程．

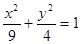(本小题满分12分)已知A,B两点是椭圆 与坐标轴正半轴的两个交点.

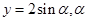(1)设为参数，求椭圆的参数方程；

(2)在第一象限的椭圆弧上求一点P，使四边形OAPB的面积最大，并求此最大值.

 

如图，四边形OABC为矩形，点A、C的坐标分别为（a+1，0）（a＞1）、（0，1），点D在OA上，坐标为（a，0），椭圆C分别以OD、OC为长、短半轴，CD是椭圆在矩形内部的椭圆弧．已知直线l：y=-x+m与椭圆弧相切，且与AD相交于点E．
（Ⅰ）当m=2时，求椭圆C的标准方程；
（Ⅱ）圆M在矩形内部，且与l和线段EA都相切，若直线l将矩形OABC分成面积相等的两部分，求圆M面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网