题目内容
已知A(-1,2)为抛物线C:y=2x2上一点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a≠-1)交抛物线C于B,交l1于D.
(1)求直线l1的方程;(2)设△ABD的面积为S,求|BD|及S的值.
1、4x+y+2=0.
2、S=S△ABD=![]() |BD||a+1|=|a+1|3(a≠-1).
|BD||a+1|=|a+1|3(a≠-1).
解析:
(1)设直线l1的方程为y-2=k(x+1),由 消去y得2x2-kx-(k+2)=0.
消去y得2x2-kx-(k+2)=0.
因直线l1与抛物线C相切,∴Δ=k2+8(k+2)=k2+8k+16=0.
解得k=-4,故切线l1的方程为y-2=-4(x+1),即4x+y+2=0.
(2)由 得点(a,2a2),由
得点(a,2a2),由![]() 得点D(a,-4a-2),
得点D(a,-4a-2),
∴|BD|=2a2+4a+2=2(a+1)2.
∴S=S△ABD=![]() |BD||a+1|=|a+1|3(a≠-1).
|BD||a+1|=|a+1|3(a≠-1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知A(1,2)为椭圆
+
=1内一点,则以A为中点的椭圆的弦所在的直线方程为( )
| x2 |
| 4 |
| y2 |
| 16 |
| A、x+2y+4=0 |
| B、x+2y-4=0 |
| C、2x+y+4=0 |
| D、2x+y-4=0 |
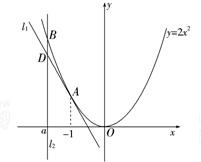 已知A(-1,2)为抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a<-1)交抛物线C于点B,交直线l1于点D.
已知A(-1,2)为抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a<-1)交抛物线C于点B,交直线l1于点D.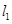 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线 :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线
 的面积为S1,求
的面积为S1,求 及S1的值.
及S1的值. 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.