题目内容
设x、y、z∈R,且5x=9y=225z,则( )
分析:令5x=9y=225z=t,则x=log5t,y=log9t,z=log225t,据选项验证可得答案.
解答:解:令5x=9y=225z=t,
则x=log5t,y=log9t,z=log225t,
∴
=logt5,
=logt9,
=logt225,
∴
+
=2logt5+logt9=logt25+logt9=logt225=
,
故选C.
则x=log5t,y=log9t,z=log225t,
∴
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
∴
| 2 |
| x |
| 1 |
| y |
| 1 |
| z |
故选C.
点评:本题考查对数的运算性质,属基础题,熟记有关运算法则是解题关键.

练习册系列答案
相关题目
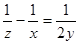 ; (2)比较3x,4y,6z的大小.
; (2)比较3x,4y,6z的大小.