题目内容
(本小题满分14分)
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.
(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足 .(
.( )
)
①求证:对于任意的 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;
②是否存在 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的 值;若不存在,说明理由.
值;若不存在,说明理由.
(1)∵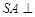 平面
平面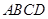 ∴
∴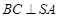 ∴
∴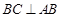 ∴
∴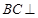 平面
平面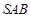 ∴平面
∴平面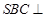 平面
平面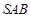 (2)①
(2)① ∴
∴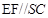
 SC∥平面AEF②
SC∥平面AEF②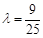
解析试题分析:(Ⅰ)∵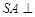 平面
平面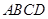 ,
,
∴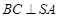 ……………1分
……………1分
∵底面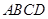 为直角梯形,
为直角梯形,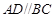 ,
,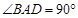 ,
,
∴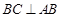 ……………2分
……………2分
∵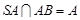
∴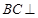 平面
平面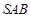 …………3分
…………3分
∵ 平面
平面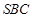
∴平面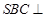 平面
平面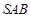 …………4分
…………4分
(Ⅱ)(ⅰ)∵ ,∴
,∴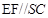 ………5分
………5分
∵ 平面
平面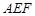 ,
, 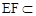 平面
平面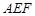 ,………6分
,………6分
∴对于任意的 ,恒有SC∥平面AEF………7分
,恒有SC∥平面AEF………7分
(ⅱ)存在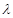 ,使得
,使得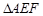 为直角三角形. ………8分
为直角三角形. ………8分
若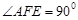 ,即
,即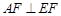
由(Ⅰ)知,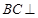 平面
平面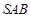 ,∵
,∵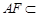 平面
平面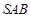 ,∴
,∴ 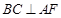 ,
,
∵ ,
,
∴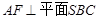 ,
,
∴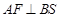 ,
,
在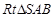 中,
中, ,
,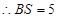 ,
,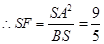 ,
,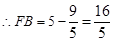 ,
, . ………10分
. ………10分
②若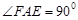 ,即
,即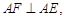 由①知,
由①知,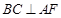 ,
,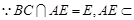 平面
平面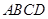 ,∴
,∴ 平面
平面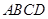 ,
,
又因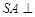 平面
平面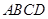 ,这与过一点有且只有一条直线与已知平面垂直相矛盾,
,这与过一点有且只有一条直线与已知平面垂直相矛盾,
∴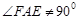 . ………12分
. ………12分
③若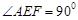 ,即
,即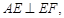 由(ⅰ)知,
由(ⅰ)知,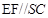 ,∴
,∴
又∵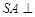 平面
平面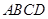 ,
,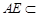 平面
平面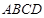 ,
,
∴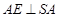 ,
,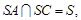 ∴
∴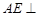 平面
平面
∴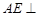
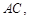 这与
这与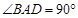 相矛盾,故
相矛盾,故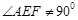
综上,当且仅当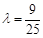 ,使得
,使得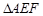 为直角三角形. ……… 14分
为直角三角形. ……… 14分
考点:线面垂直平行的判定
点评:第二小题②采用空间向量求解比较简单

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
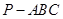 中,
中,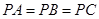 ,
,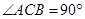 ,
,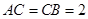 .
. 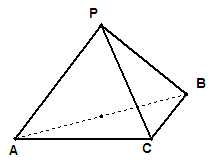
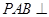 平面
平面 ;
;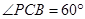 时,求三棱锥
时,求三棱锥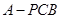 的体积.
的体积. 为圆
为圆 的直径,点
的直径,点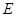 、
、 在圆
在圆 ,矩形
,矩形 所在的平面与圆
所在的平面与圆 ,
, .
.
 平面
平面 ;
;  的长为何值时,平面
的长为何值时,平面 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为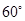 ?
? 点
点 上,过点
上,过点 做
做 //
// 将
将 的位置(
的位置( ),
), .
.
 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由. ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA
 与
与 均为菱形,
均为菱形,  ,且
,且 ,
,
 平面
平面 ;
; 的余弦值。
的余弦值。
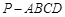 中,
中,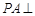 平面
平面 ,
,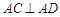 ,
,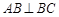 ,
,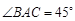 ,
,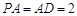 ,
,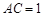 .
.
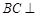 平面
平面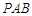
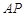 和平面
和平面 所成角的正弦值
所成角的正弦值 的正切值;
的正切值;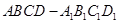 中,
中,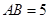 ,
,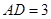 ,
,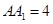 ,
,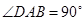 ,
,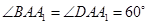 ,
, 是
是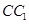 的中点,设
的中点,设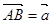 ,
,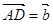 ,
, .
.
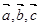 表示
表示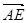 ;
; 的长.
的长.