题目内容
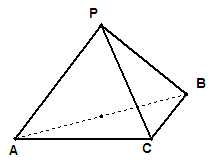
(本题满分12分)三棱锥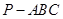 中,
中,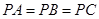 ,
,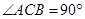 ,
,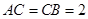 .
. 
(Ⅰ)求证:平面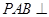 平面
平面 ;
;
(Ⅱ)当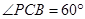 时,求三棱锥
时,求三棱锥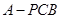 的体积.
的体积.
(1)先证明 平面
平面 ,然后利用面面垂直的判定定理得到证明。
,然后利用面面垂直的判定定理得到证明。
(2)
解析试题分析:证明:(Ⅰ)作 平面
平面 于点
于点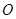 ,∵
,∵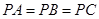 ,
,
∴ ,即
,即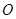 为
为 的外心
的外心
又∵ 中,
中,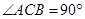
故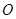 为
为 边的中点
边的中点
所以 平面
平面
即证:平面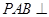 平面
平面 . .......6分
. .......6分
(Ⅱ)∵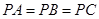 ,
,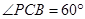 ,∴
,∴ 为正三角形
为正三角形
∵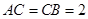 , ∴
, ∴
∴

∴三棱锥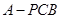 的体积
的体积
 .………….12分
.………….12分
考点:本试题主要是考查了面面垂直以及棱锥的体积的求解。
点评:解决该试题的关键是能利用面面垂直的判定定理和等体积法来分别求解得到。同时也可以建立空间直角坐标系来证明垂直问题,通过法向量垂直来说明面面垂直,同时利用向量可以求点到面的距离,进而得到体积的运算。属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
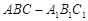 中,△
中,△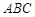 为等腰直角三角形,∠
为等腰直角三角形,∠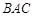 =
=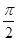 ,且
,且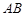 =
=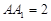 ,
,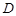 、
、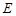 、
、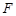 分别为
分别为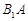 、
、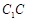 、
、 的中点.
的中点.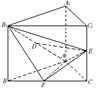
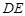 ∥平面
∥平面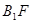 ⊥平面
⊥平面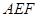 ;
;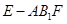 的体积.
的体积.
 中,侧棱
中,侧棱 底面
底面 ,
, ,
,
 ,
,
 与
与 所成角的余弦值;
所成角的余弦值;
 中,侧面
中,侧面
 底面ABC,侧面
底面ABC,侧面 ,E、F分别是
,E、F分别是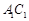 、AB的中点.
、AB的中点.
 ;
; 关于直线
关于直线 对称,
对称, ,
, ,
, .把
.把 沿
沿 折起(如图2),使二面角
折起(如图2),使二面角 的余弦值等于
的余弦值等于 .
.
 两点间的距离;
两点间的距离; 平面
平面 ;
; 中,
中, 底面
底面 ,点
,点 ,
, 分别在棱
分别在棱 上,且
上,且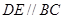

 平面
平面 ;
; 的中点时,求
的中点时,求 与平面
与平面 为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
为直二面角?若存在,请确定点E的位置;若不存在,请说明理由. ,D是A1B1中点.
,D是A1B1中点.

 .(
.( )
) ,恒有SC∥平面AEF;
,恒有SC∥平面AEF; ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的