题目内容
10.已知点A(0,5)是椭圆$\frac{{x}^{2}}{98}$+$\frac{{y}^{2}}{49}$=1内一定点,P是这个椭圆上的点,要使|PA|的值最大,则P的坐标应是$(±4\sqrt{3},-5)$,|PA|的最大值等于2$\sqrt{37}$.分析 设P$(7\sqrt{2}cosθ,7sinθ)$(θ∈[0,2π)).可得|PA|=$\sqrt{(7\sqrt{2}cosθ)^{2}+(7sinθ-5)^{2}}$=$\sqrt{-49(sinθ+\frac{5}{7})^{2}+148}$,利用二次函数与三角函数的单调性即可得出.
解答 解:设P$(7\sqrt{2}cosθ,7sinθ)$(θ∈[0,2π)).
则|PA|=$\sqrt{(7\sqrt{2}cosθ)^{2}+(7sinθ-5)^{2}}$=$\sqrt{-49si{n}^{2}θ-70sinθ+123}$=$\sqrt{-49(sinθ+\frac{5}{7})^{2}+148}$≤2$\sqrt{37}$,当sinθ=-$\frac{5}{7}$时取等号,
∴$cosθ=±\frac{2\sqrt{6}}{7}$.
∴P$(±4\sqrt{3},-5)$.
故答案分别为:$(±4\sqrt{3},-5)$;2$\sqrt{37}$.
点评 本题考查了椭圆的标准方程及参数方程、二次函数与三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知直线l1经过A(-1,4),B(-6,-1)两点,直线l2倾斜角为135°,那么l1与l2( )
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 相交但不垂直 |
5.已知抛物线y2=4x,过焦点且倾斜角为60°的直线与抛物线交于A、B两点,则△AOB的面积为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{8\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |

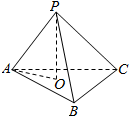 三棱锥P-ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证:
三棱锥P-ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证: