题目内容
20．已知：如图，在△ABC中，AC=13，BC=14，AB=15，求△ABC外接圆⊙O的半径r．
分析 作直径AD，连接BD，根据余弦定理求出cosC，根据正弦的定义求出圆的直径，得到答案．
解答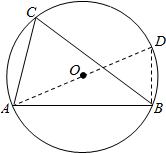 
解：作直径AD，连接BD，
∵AC=13，BC=14，AB=15，
∴152=132+142-2×13×14×cosC，
∴cosC=$\frac{5}{13}$，
∴sinC=$\frac{12}{13}$
∵∠D=∠C，
∴sinD=$\frac{12}{13}$
∴AD=$\frac{13}{\frac{12}{13}}$=$\frac{169}{12}$，
∴△ABC外接圆⊙O的半径r为$\frac{169}{24}$．
点评 本题考查的是三角形外接圆和外心的概念，掌握余弦定理和圆周角定理是解题的关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
12．已知f（x），g（x）都是R上的奇函数，f（x）＞0的解集为（a2，b），g（x）＞0的解集为（$\frac{{a}^{2}}{2}$，$\frac{b}{2}$），且a2＜$\frac{b}{2}$，则f（x）•g（x）＞0的解集为（ ）
| A． | （-$\frac{b}{2}$，-a2）∪（a2，$\frac{b}{2}$） | B． | （-$\frac{b}{2}$，a2）∪（-a2，$\frac{b}{2}$） | C． | （-$\frac{b}{2}$，-a2）∪（a2，b） | D． | （-b，-a2）∪（a2，$\frac{b}{2}$） |
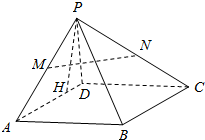如图，四棱锥P-ABCD，底面ABCD为正方形，平面PAD⊥平面ABCD，PA=$\sqrt{3}$，PD=1，AD=2，PH⊥AD交AD于H．