题目内容
过点(5,0)的椭圆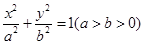 与双曲线
与双曲线 有共同的焦点,
有共同的焦点,
则该椭圆的短轴长为( )
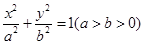 与双曲线
与双曲线 有共同的焦点,
有共同的焦点,则该椭圆的短轴长为( )
A.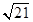 | B. | C.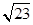 | D.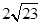 |
B
因为椭圆与双曲线有共同焦点 ,所以
,所以 。因为椭圆经过点
。因为椭圆经过点 ,所以
,所以 ,可得
,可得 ,所以
,所以 ,从而可得椭圆的短轴长为
,从而可得椭圆的短轴长为 ,故选B
,故选B
 ,所以
,所以 。因为椭圆经过点
。因为椭圆经过点 ,所以
,所以 ,可得
,可得 ,所以
,所以 ,从而可得椭圆的短轴长为
,从而可得椭圆的短轴长为 ,故选B
,故选B
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
题目内容
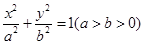 与双曲线
与双曲线 有共同的焦点,
有共同的焦点,A.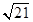 | B. | C.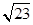 | D.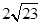 |
 ,所以
,所以 。因为椭圆经过点
。因为椭圆经过点 ,所以
,所以 ,可得
,可得 ,所以
,所以 ,从而可得椭圆的短轴长为
,从而可得椭圆的短轴长为 ,故选B
,故选B
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案