题目内容
对任何实数x,y,函数f(x)满足f(x+y)=f(x)•f(y),且f(1)=2,则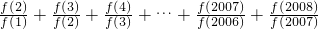 =________.
=________.
4014
分析:令x=1,y=n代入关系式得到 为一个定值,构造一个常数列,再代入所求的和式进行求值即可.
为一个定值,构造一个常数列,再代入所求的和式进行求值即可.
解答:令x=1,y=n代入f(x+y)=f(x)•f(y)得,f(n+1)=f(n)•f(1),
∵f(1)=2,∴ =f(1)=2,
=f(1)=2,
∴数列{ }是有无穷个2构成的常数列,
}是有无穷个2构成的常数列,
∴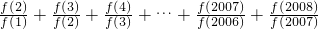 =2007×2=4014,
=2007×2=4014,
故答案为:4014.
点评:本题考查了抽象函数和数列求和问题,先由关系式利用“赋值法”得到,f(n+1)与f(n)的关系式,构造出一个特殊数列,再进行求和.
分析:令x=1,y=n代入关系式得到
 为一个定值,构造一个常数列,再代入所求的和式进行求值即可.
为一个定值,构造一个常数列,再代入所求的和式进行求值即可.解答:令x=1,y=n代入f(x+y)=f(x)•f(y)得,f(n+1)=f(n)•f(1),
∵f(1)=2,∴
 =f(1)=2,
=f(1)=2,∴数列{
 }是有无穷个2构成的常数列,
}是有无穷个2构成的常数列,∴
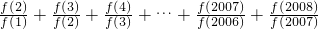 =2007×2=4014,
=2007×2=4014,故答案为:4014.
点评:本题考查了抽象函数和数列求和问题,先由关系式利用“赋值法”得到,f(n+1)与f(n)的关系式,构造出一个特殊数列,再进行求和.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
 = .
= .