题目内容
设函数f（x）=sinx+cosx，g（x）=f（x）•f′（x）+[f（x）]2．
（1）求g（x）的周期和对称中心；
（2）求g（x）在[-
，
]上值域．
（1）求g（x）的周期和对称中心；
（2）求g（x）在[-
| π |
| 4 |
| π |
| 4 |
分析：求出函数的导数．利用三角函数的周期公式和对称中心的性质分别进行求解即可．
解答：解：（1）f'（x）=cosx-sinx，所以g（x）=f（x）•f′（x）+[f（x）]2
=（sinx+cosx）（cosx-sinx）+（cosx+sinx）2=cos2x+sin2x+1=
sin?(2x+
)+1，
所以函数g（x）的周期T=π．
由2x+
=kπ 得 x=-
+
，k∈Z
所以g（x）的对称中心为(-
+
，0)，k∈Z．
（2）因为x∈[-
，
]，所以2x+
∈[-
，
]，sin?(2x+
)∈[-
，1]
所以g（x）∈[0，
+1]．
=（sinx+cosx）（cosx-sinx）+（cosx+sinx）2=cos2x+sin2x+1=
| 2 |
| π |
| 4 |
所以函数g（x）的周期T=π．
由2x+
| π |
| 4 |
| π |
| 8 |
| kπ |
| 2 |
所以g（x）的对称中心为(-
| π |
| 8 |
| kπ |
| 2 |
（2）因为x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
所以g（x）∈[0，
| 2 |
点评：本题主要考查导数的基本运算，考查三角函数的图象和性质，考查学生的基本运算能力．
练习册系列答案
阅读快车系列答案
相关题目
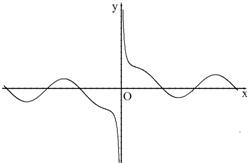如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g （ x ）=| 1 |
| x |
A、
| ||
| B、f（x）g（x） | ||
| C、f（x）-g（x） | ||
| D、f（x）+g（x） |
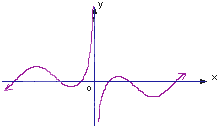设函数f（x）=sinx，g（x）=