Question

（2011•杭州一模）设函数f（x）=

sinx+cosx-|sinx-cosx|

2

（x∈R），若在区间[0，m]上方程f（x）=-

3

2

恰有4个解，则实数m的取值范围是

[

5π

3

，

17π

6

)

．

Answer 1

分析：解：先画出函数f（x）在一个周期上的图象，再将方程f（x）=-

3

2

恰有4个解问题转化为函数f（x）的图象与y=-

3

2

恰有4个交点问题，数形结合即可求得m的范围

解答：解：当sinx≥cosx时，即x∈[

π

4

+2kπ，

5π

4

+2kπ]时，f（x）=cosx
当sinx＜cosx时，即x∈[-

3π

4

+2kπ，

π

4

+2kπ]时，f（x）=sinx
∴函数f（x）为以2π为周期的周期函数，其在[0，2π）上的图象如图：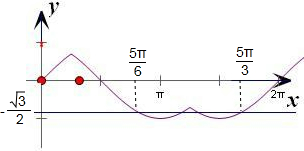
若在区间[0，m]上方程f（x）=-

3

2

恰有4个解，即在区间[0，m]上函数f（x）的图象与y=-

3

2

恰有4个交点
∵f（

5π

6

）=-

3

2

，f（

5π

3

）=-

3

2

，f（

5π

6

+2π）=f（

17π

6

）=-

3

2

∴由图数形结合可知，当m∈[

5π

3

，

17π

6

)时，两函数图象恰有4个交点
故答案为 [

5π

3

，

17π

6

)

点评：本题主要考查了三角分段函数的图象及其画法，方程的根与函数图象交点间的关系，数形结合求参数的范围及转化化归的思想方法