题目内容
12.下列说法中正确的个数为2.①命题:“若a<0,则a2≥0”的否命题是“若a≥0,则a2<0”;
②若复合命题“p∧q”为假命题,则p,q均为假命题;
③“三个数a,b,c成等比数列”是“$b=\sqrt{ac}$”的充分不必要条件;
④命题“若x=y,则sinx=siny”的逆否命题为真命题.
分析 写出原命题的否命题,可判断①;根据复合命题真假判断的真值表,可判断②;根据等比数列的定义及充要条件的定义,可判断③;根据互为逆否的两个命题,真假性相同,可判断④
解答 解:①命题:“若a<0,则a2≥0”的否命题是“若a≥0,则a2<0”,故正确;
②若复合命题“p∧q”为假命题,则p,q存在假命题,但不一定均为假命题,故错误;
③“三个数a,b,c成公比为负的等比数列”时,“$b=\sqrt{ac}$”不成立,
“$b=\sqrt{ac}$=0”时,“三个数a,b,c成等比数列”不成立,
故“三个数a,b,c成等比数列”是“$b=\sqrt{ac}$”的即不充分不必要条件,故错误;
④命题“若x=y,则sinx=siny”为真命题,故其逆否命题为真命题,故正确.
综上所述,正确的命题个数为2个,
故答案为:2
点评 本题考查的知识点是命题的真假判断与应用,四种命题,复合命题,充要条件,难度中档.

练习册系列答案
相关题目
2.已知函数$f(x)=\sqrt{3}sinωx+cosωx(ω>0)$的最小正周期为π.对于函数f(x),下列说法正确的是( )
| A. | 在$[\frac{π}{6},\frac{2π}{3}]$上是增函数 | |
| B. | 图象关于直线$x=\frac{5π}{12}$对称 | |
| C. | 图象关于点$(-\frac{π}{3},0)$对称 | |
| D. | 把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个单位,所得函数图象关于y轴对称 |
20.若sinα>0,则( )
| A. | cos2α>0 | B. | tan2α>0 | C. | $cos\frac{α}{2}>0$ | D. | $tan\frac{α}{2}>0$ |
7.已知$a={log_{\frac{1}{5}}}\frac{1}{3},b={log_5}\frac{1}{3},c={(\frac{1}{5})^{\frac{1}{2}}}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
17.已知函数f(x)=cos4x-sin4x,下列结论错误的是( )
| A. | f(x)=cos2x | B. | 函数f(x)的图象关于直线x=0对称 | ||
| C. | f(x)的最小正周期为π | D. | f(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] |
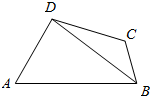 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.