题目内容
(2011•浙江)已知公差不为0的等差数列{an}的首项a1为a(a∈R)设数列的前n项和为Sn,且 ,
, ,
,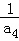 成等比数列.
成等比数列.
(1)求数列{an}的通项公式及Sn;
(2)记An= +
+ +
+ +…+
+…+ ,Bn=
,Bn= +
+ +…+
+…+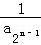 ,当n≥2时,试比较An与Bn的大小.
,当n≥2时,试比较An与Bn的大小.
 ,
, ,
,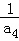 成等比数列.
成等比数列.(1)求数列{an}的通项公式及Sn;
(2)记An=
 +
+ +
+ +…+
+…+ ,Bn=
,Bn= +
+ +…+
+…+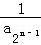 ,当n≥2时,试比较An与Bn的大小.
,当n≥2时,试比较An与Bn的大小.(1)an=na 
(2)当a>0时,An<Bn;当a<0时,An>Bn

(2)当a>0时,An<Bn;当a<0时,An>Bn
(1)设等差数列{an}的公差为d,由(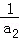 )2=
)2= •
• ,
,
得(a1+d)2=a1(a1+3d),因为d≠0,所以d=a1=a
所以an=na,Sn=
(2)解:∵ =
=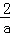 (
( ﹣
﹣ )
)
∴An= +
+ +
+ +…+
+…+ =
=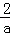 (1﹣
(1﹣ )
)
∵ =2n﹣1a,所以
=2n﹣1a,所以 =
= =
= 为等比数列,公比为
为等比数列,公比为 ,
,
Bn= +
+ +…+
+…+ =
= •
• =
= •(1﹣
•(1﹣ )
)
当n≥2时,2n=Cn0+Cn1+…+Cnn>n+1,即1﹣ <1﹣
<1﹣
所以,当a>0时,An<Bn;当a<0时,An>Bn.
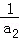 )2=
)2= •
• ,
,得(a1+d)2=a1(a1+3d),因为d≠0,所以d=a1=a
所以an=na,Sn=

(2)解:∵
 =
=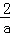 (
( ﹣
﹣ )
)∴An=
 +
+ +
+ +…+
+…+ =
=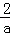 (1﹣
(1﹣ )
)∵
 =2n﹣1a,所以
=2n﹣1a,所以 =
= =
= 为等比数列,公比为
为等比数列,公比为 ,
,Bn=
 +
+ +…+
+…+ =
= •
• =
= •(1﹣
•(1﹣ )
)当n≥2时,2n=Cn0+Cn1+…+Cnn>n+1,即1﹣
 <1﹣
<1﹣
所以,当a>0时,An<Bn;当a<0时,An>Bn.

练习册系列答案
相关题目
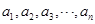 为
为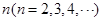 阶“期待数列”:
阶“期待数列”: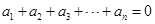 ,②
,②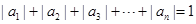 .
.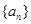 为
为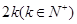 阶“期待数列”,求公比
阶“期待数列”,求公比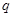 ;
;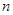 阶“期待数列”
阶“期待数列”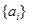 的前
的前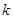 项和为
项和为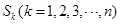 .
.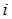 )求证:
)求证: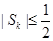 ;
;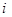
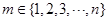 ,使
,使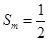 ,试问数列
,试问数列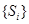
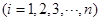 是否为
是否为 是首项
是首项 ,公比为
,公比为 的等比数列,
的等比数列,

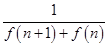 ,n∈N*.记数列{an}的前n项和为Sn,则S2013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2013=( ) -1
-1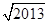 -1
-1 -1
-1 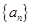 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足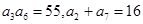 .
.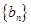 满足等式:
满足等式: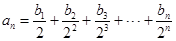 (n为正整数)求数列
(n为正整数)求数列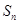 .
.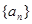 中,
中,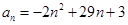 (
(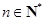 ),那么此数列
),那么此数列 的公差大于零,且
的公差大于零,且 是方程
是方程 的两个根;各项均为正数的等比数列
的两个根;各项均为正数的等比数列 的前
的前 项和为
项和为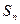 ,且满足
,且满足 ,
,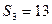
 满足
满足 ,求数列
,求数列 .
.