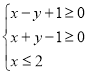题目内容
【题目】已知椭圆C：
1（a＞b＞0）的左、右焦点分别为F1、F2，点P（﹣1，
）在椭圆C上，且|PF2|
．
（1）求椭圆C的方程；
（2）过点F2的直线l与椭圆C交于A，B两点，M为线段AB的中点，若椭圆C上存在点N，满足
3
（O为坐标原点），求直线l的方程．
【答案】（1）
．（2）x
y﹣1＝0或x
y﹣1＝0．
【解析】
（1）根据题意得
①，
②，
③，由①②③组成方程组，解得
，
，进而得椭圆
的方程．
（2）设直线
的方程为
，
，
，
，
，联立直线与椭圆的方程得关于
的一元二次方程，结合韦达定理得
，
，从而得线段
中点
坐标，点
的坐标，将其代入椭圆方程，可解得
，进而得出直线的方程．
解：（1）因为点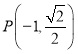
在椭圆上，且
．
所以，①
，解得
，②
又因为③
由①②③组成方程组，解得
，
，
所以椭圆的方程为：
．
（2）由（1）可知
，
设直线的方程为，，，，，
联立直线与椭圆的方程得
，
得，则，
所以线段中点
，
，
所以
，，
所以点的坐标为
，
，
将点坐标代入椭圆的方程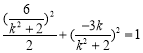
，
解得
，
，
所以直线的方程为：
或
．
练习册系列答案
相关题目
