题目内容
设Sn=
证明:|Sm-Sn|=|![]() |
|
≤|![]() |+|
|+|![]() |+…+|
|+…+|![]() |.
|.
∵|sin(n+1)|≤1,|sin(n+2)|≤1,…,|sinm|≤1,
∴上式≤|![]() |+|
|+|![]() |+…+|
|+…+|![]() |
|
=![]() +
+![]() +…+
+…+![]()
=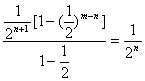 [1-(
[1-(![]() )m-n]<
)m-n]<![]() .
.
∴原不等式成立.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
题目内容
设Sn=
证明:|Sm-Sn|=|![]() |
|
≤|![]() |+|
|+|![]() |+…+|
|+…+|![]() |.
|.
∵|sin(n+1)|≤1,|sin(n+2)|≤1,…,|sinm|≤1,
∴上式≤|![]() |+|
|+|![]() |+…+|
|+…+|![]() |
|
=![]() +
+![]() +…+
+…+![]()
=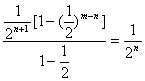 [1-(
[1-(![]() )m-n]<
)m-n]<![]() .
.
∴原不等式成立.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案