题目内容
设数列{
}前n项和为Sn,则S1=
,S2=
,S3=
,S4=
,并由此猜想出Sn=
.
| n |
| (n+1)! |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
| 5 |
| 6 |
| 23 |
| 24 |
| 23 |
| 24 |
| 119 |
| 120 |
| 119 |
| 120 |
| (n+1)!-1 |
| (n+1)! |
| (n+1)!-1 |
| (n+1)! |
分析:由已知,直接计算各项,并进行归纳推理即可.
解答:解:则S1=
=
S2=
+
=
S3=
+
=
S4=
+
=
由此猜想出Sn=
故答案为:
.
| 1 |
| 2! |
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 2 |
| 3! |
| 5 |
| 6 |
S3=
| 5 |
| 6 |
| 3 |
| 4! |
| 23 |
| 24 |
S4=
| 23 |
| 24 |
| 4 |
| 5! |
| 119 |
| 120 |
由此猜想出Sn=
| (n+1)!-1 |
| (n+1)! |
故答案为:
| 1 |
| 2 |
| 5 |
| 6 |
| 23 |
| 24 |
| 119 |
| 120 |
| (n+1)!-1 |
| (n+1)! |
点评:本题考查归纳推理,数字规律探求的能力.实际上可看作给出一个数列的前几项写出数列的通项公式.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
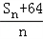 的最小值;
的最小值;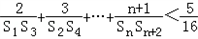 ;
;