题目内容
已知sinα=
,且α=(
,π),求cos2α,sin2α及sin
的值.
| 5 |
| 13 |
| π |
| 2 |
| α |
| 2 |
考点:半角的三角函数,二倍角的正弦,二倍角的余弦
专题:三角函数的求值
分析:利用同角三角函数间的关系式及二倍角的正弦、余弦及半角公式即可求得cos2α,sin2α及sin
的值.
| α |
| 2 |
解答:
解:∵sinα=
,且α=(
,π),
∴cosα=-
=-
,
∴cos2α=1-2sin2α=1-
=
,sin2α=2sinαcosα=-
,
由α∈(
,π)知,
∈(
,
),
∴sin
=
=
=
.
| 5 |
| 13 |
| π |
| 2 |
∴cosα=-
| 1-sin2α |
| 12 |
| 13 |
∴cos2α=1-2sin2α=1-
| 50 |
| 169 |
| 119 |
| 169 |
| 120 |
| 169 |
由α∈(
| π |
| 2 |
| α |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴sin
| α |
| 2 |
|
|
5
| ||
| 26 |
点评:本题考查同角三角函数间的关系式及二倍角的正弦、余弦及半角公式的应用,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
已知A、B分别为椭圆x2+
=1的左右顶点,P是椭圆上第一象限的任一点,若∠PAB=α,∠PBA=β,则必有( )
| y2 |
| 2 |
| A、2tanα+cotβ=0 |
| B、2tanα-cotβ=0 |
| C、tanα+2cotβ=0 |
| D、tanα-2cosβ=0 |
已知p:?x∈R,x2≥0,q:?x0∈R,sinx0=
,则下列判断中,错误的是( )
| 2 |
| A、p或q为真,非p为假 |
| B、p或q为真,非q为假 |
| C、p且q为假,非p为假 |
| D、p且q为假,非q为真 |
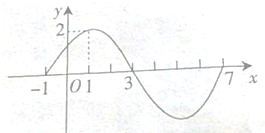 如图为函数y1=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-
如图为函数y1=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-