题目内容
数列{2n-1}的前n项1,3,7,…,2n-1组成集合 ,从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn.例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7.则当n=3时,S3= ;试写出Sn= .
,从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn.例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7.则当n=3时,S3= ;试写出Sn= .
【答案】分析:根据Sn=T1+T2+…+Tn的意义即可求得n=3时S3.根据S1,S2,S3,猜想 -1,然后利用数学归纳法证明即可.
-1,然后利用数学归纳法证明即可.
解答:解:当n=3时,A3={1,3,7},
T1=1+3+7=11,T2=1×3+1×7+3×7=31,T3=1×3×7=21,
所以S3=11+31+21=63;
由S1=1=21-1= -1,S2=7=23-1=
-1,S2=7=23-1= -1,S3=63=26-1=
-1,S3=63=26-1= -1,猜想
-1,猜想 -1,下面证明:
-1,下面证明:
(1)易知n=1时成立;
(2)假设n=k时 -1,
-1,
则n=k+1时,Sk+1=T1+T2+T3+…+Tk+1
=[T1′+(2k+1-1)]+[T2′+(2k+1-1)T1′]+[T3′+(2k+1-1)T2′]+…+[Tk′+(2k+1-1) ](其中Ti′,i=1,2,…,k,为n=k时可能的k个数的乘积的和为Tk),
](其中Ti′,i=1,2,…,k,为n=k时可能的k个数的乘积的和为Tk),
=( )+(2k+1-1)+(2k+1-1)(
)+(2k+1-1)+(2k+1-1)( )
)
=Sk+(2k+1-1)+(2k+1-1)Sk
=2k+1( -1)+(2k+1-1)
-1)+(2k+1-1)
= -1=
-1= -1,即n=k时
-1,即n=k时 -1也成立,
-1也成立,
综合(1)(2)知对n∈N* -1成立.
-1成立.
所以 -1.
-1.
故答案为:63; -1.
-1.
点评:本题考查等差、等比数列的综合,考查合情推理,考查学生分析解决问题的能力,具有一定综合性,难度较大,能力要求较高.
 -1,然后利用数学归纳法证明即可.
-1,然后利用数学归纳法证明即可.解答:解:当n=3时,A3={1,3,7},
T1=1+3+7=11,T2=1×3+1×7+3×7=31,T3=1×3×7=21,
所以S3=11+31+21=63;
由S1=1=21-1=
 -1,S2=7=23-1=
-1,S2=7=23-1= -1,S3=63=26-1=
-1,S3=63=26-1= -1,猜想
-1,猜想 -1,下面证明:
-1,下面证明:(1)易知n=1时成立;
(2)假设n=k时
 -1,
-1,则n=k+1时,Sk+1=T1+T2+T3+…+Tk+1
=[T1′+(2k+1-1)]+[T2′+(2k+1-1)T1′]+[T3′+(2k+1-1)T2′]+…+[Tk′+(2k+1-1)
 ](其中Ti′,i=1,2,…,k,为n=k时可能的k个数的乘积的和为Tk),
](其中Ti′,i=1,2,…,k,为n=k时可能的k个数的乘积的和为Tk),=(
 )+(2k+1-1)+(2k+1-1)(
)+(2k+1-1)+(2k+1-1)( )
)=Sk+(2k+1-1)+(2k+1-1)Sk
=2k+1(
 -1)+(2k+1-1)
-1)+(2k+1-1)=
 -1=
-1= -1,即n=k时
-1,即n=k时 -1也成立,
-1也成立,综合(1)(2)知对n∈N*
 -1成立.
-1成立.所以
 -1.
-1.故答案为:63;
 -1.
-1.点评:本题考查等差、等比数列的综合,考查合情推理,考查学生分析解决问题的能力,具有一定综合性,难度较大,能力要求较高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在数列{2n-1}的前2011项中任意选取若干项相乘(当只取到一项时,乘积就为所选项本身),记所有这样的乘积和为S,则log2(S+1)的值为( )
| A、1005×2011 | B、1006×2011 | C、2010×2011 | D、2011×2011 |
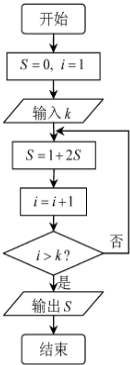 (2013•福建)阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( )
(2013•福建)阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( ) (2011•通州区一模)对于数列{2n-1}的前10项a1,a2,…,a10,如果遵循右侧算法框图的运算,那么输出的结果s=
(2011•通州区一模)对于数列{2n-1}的前10项a1,a2,…,a10,如果遵循右侧算法框图的运算,那么输出的结果s=