题目内容
设抛物线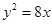 的焦点为
的焦点为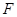 ,准线为
,准线为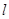 ,
,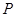 为抛物线上一点,
为抛物线上一点,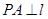 ,
,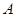 为垂足.如果直线
为垂足.如果直线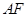 的斜率为
的斜率为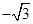 ,那么
,那么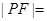
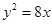 的焦点为
的焦点为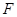 ,准线为
,准线为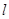 ,
,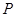 为抛物线上一点,
为抛物线上一点,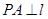 ,
,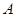 为垂足.如果直线
为垂足.如果直线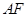 的斜率为
的斜率为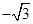 ,那么
,那么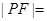
A.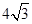 | B.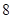 | C.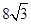 | D.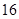 |
B
:∵抛物线方程为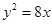 ,∴焦点F(2,0),准线l方程为x=-2,
,∴焦点F(2,0),准线l方程为x=-2,
∵直线AF的斜率为- 3 ,直线AF的方程为y="-" 3 (x-2),由 x="-2" y="-" 3 (x-2) 可得A点坐标为(-2,4 3 )∵PA⊥l,A为垂足,∴P点纵坐标为4 3 ,代入抛物线方程,得P点坐标为(6,4 3 ),∴|PF|=|PA|=6-(-2)=8,故选B
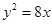 ,∴焦点F(2,0),准线l方程为x=-2,
,∴焦点F(2,0),准线l方程为x=-2,∵直线AF的斜率为- 3 ,直线AF的方程为y="-" 3 (x-2),由 x="-2" y="-" 3 (x-2) 可得A点坐标为(-2,4 3 )∵PA⊥l,A为垂足,∴P点纵坐标为4 3 ,代入抛物线方程,得P点坐标为(6,4 3 ),∴|PF|=|PA|=6-(-2)=8,故选B

练习册系列答案
相关题目
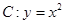 的焦点为
的焦点为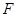 ,动点
,动点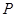 在直线
在直线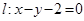 上
上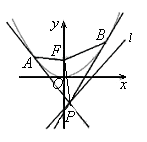
 的直线
的直线 与抛物线
与抛物线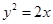 相交于
相交于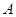 、
、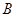 两点,且
两点,且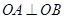 ,
,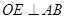 于
于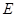 .
.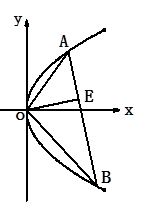
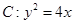 ,过点
,过点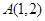 作抛物线
作抛物线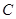 的弦
的弦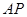 ,
,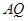 .
.
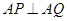 ,证明直线
,证明直线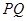 过定点,并求出定点的坐标;
过定点,并求出定点的坐标;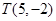 ,请问是否存在以
,请问是否存在以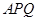 ? 若存在,求出
? 若存在,求出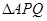 的个数?如果不存在,请说明理由.
的个数?如果不存在,请说明理由.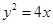 的准线为
的准线为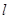 ,
,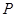 为抛物线上的点,
为抛物线上的点,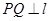 ,垂足为
,垂足为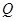 ,若
,若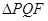 得面积与
得面积与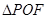 的面积之比为
的面积之比为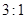 ,则
,则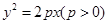 有一内接直角三角形,直角的顶点在原点,一直角边的方程是
有一内接直角三角形,直角的顶点在原点,一直角边的方程是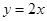 ,斜边长是
,斜边长是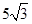 ,求此抛物线的方程。
,求此抛物线的方程。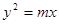
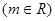 的焦点为
的焦点为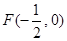 ,过点
,过点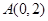 的直线
的直线 与抛物线
与抛物线 的焦点坐标是( )
的焦点坐标是( )