题目内容
已知直线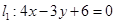 和直线
和直线 ,则抛物线
,则抛物线 上的动点
上的动点 到直线
到直线 和
和 的距离之和的最小值为___________.
的距离之和的最小值为___________.

解析试题分析:设抛物线 上的动点
上的动点 的坐标为
的坐标为 ,它到到直线
,它到到直线 和
和 的距离之和为
的距离之和为 ,则
,则
 =
= ,当
,当 时,
时, .
.
考点:直线与抛物线的位置关系及二次函数的最值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是
| A.直线 | B.椭圆 | C.抛物线 | D.双曲线 |
已知P为双曲线 左支上一点,
左支上一点, 为双曲线的左右焦点,且
为双曲线的左右焦点,且 则此双曲线离心率是( )
则此双曲线离心率是( )
A. | B.5 | C.2 | D.3 |
若 ,则“
,则“ ”是“方程
”是“方程 表示双曲线”的( )
表示双曲线”的( )
| A.必要不充分条件 | B..充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件. |
 经过伸缩变换
经过伸缩变换 后,得到的曲线方程是_________ .
后,得到的曲线方程是_________ . 的左、右焦点分别为F1,F2,线段F1F2被抛物线
的左、右焦点分别为F1,F2,线段F1F2被抛物线 的焦点分成5:3两段,则此双曲线的离心率为______.
的焦点分成5:3两段,则此双曲线的离心率为______. 中,已知中心在坐标原点的双曲线
中,已知中心在坐标原点的双曲线 经过点
经过点 ,且它的右焦点
,且它的右焦点 与抛物线
与抛物线 的焦点相同,则该双曲线的标准方程为 .
的焦点相同,则该双曲线的标准方程为 . 的渐近线方程是_________________.
的渐近线方程是_________________.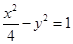 的离心率等于____________.
的离心率等于____________.