题目内容
1.已知集合M={-1,0,1,2,3},N={x|x2-2x≤0},则M∩N=( )| A. | {1,2} | B. | {2,3} | C. | {-1,0,3} | D. | {0,1,2} |
分析 求出N中不等式的解集确定出N,找出M与N的交集即可.
解答 解:由N中不等式变形得:x(x-2)≤0,
解得:0≤x≤2,即N=[0,2],
∵M={-1,0,1,2,3},
∴M∩N={0,1,2},
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
9.集合$A=\left\{{x\left|{\frac{x+2}{x-2}≤0}\right.}\right\}$,B={x|x-1≥0},则A∩B为( )
| A. | [1,2] | B. | [1,2) | C. | [-2,∞) | D. | (-2,2] |
6.复数$z=\frac{10i}{1+3i}$(其中i为虚数单位),$\overline z$为z的共轭复数,则下列结论正确的是( )
| A. | z=-3+i | B. | $\overline z=3-i$ | C. | z=1-3i | D. | $\overline z=-1+3i$ |
10.已知f(x)为偶函数,在[0,+∞)上f(x)=$\left\{\begin{array}{l}{a({x}^{3}-1),x∈[0,1]}\\{x+\frac{a}{x}-2,x∈(1,+∞)}\end{array}\right.$且为单调递增函数,则使得f(ax)>f(2x-1)成立的x的取值范围是( )
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,1) | D. | D、(-∞,$-\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
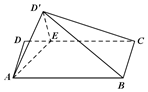 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.