题目内容
已知10条狗的血球体积及红血球数的测量值如下：血球体积x(mL) | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
红血球数y(百万) | 6.53 | 6.30 | 9.52 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 8.72 |
（1）画出上表的散点图；
（2）求出回归直线的方程.
解：（1）散点图如下.
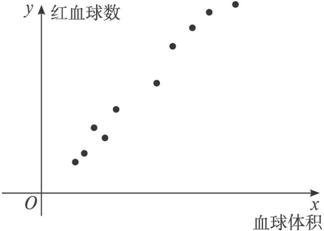
（2）
(45+42+46+48+42+35+58+40+39+50)=44.50,
(6.53+6.30+9.52+7.50+6.99+5.90+9.49+6.20+6.55+8.72)=7.37.
设回归直线方程为
=bx+a,则b=
=0.175,a=
=-0.418,
所以所求回归直线的方程为
=0.175x-0.148.
点评：对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数a,b的计算公式,算出a,b．由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误,求线性回归方程的步骤：计算平均数
；计算xi与yi的积,求∑xiyi；计算∑xi2；将结果代入公式求b；用a=
求a；写出回归直线方程．
| x | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
| y | 6.53 | 6.30 | 9.25 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 7.72 |
（1）画出上表的散点图；
（2）求出回归直线并且画出图形
（3）回归直线必经过的一点是哪一点？
X | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
y | 6.35 | 6.30 | 9.25 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 7.72 |
其中ｘ为（血球体积，mm），ｙ为（血红球数，百万）
（1）画出上表的散点图;
（2）求出回归直线并且画出图形;
已知10只狗的血球体积及红血球的测量值如下
|
|
|
| 45 | 6.53 |
| 42 | 6.30 |
| 46 | 9.25 |
| 48 | 7.50 |
| 42 | 6.99 |
| 35 | 5.90 |
| 58 | 9.49 |
| 40 | 6.20 |
| 39 | 6.55 |
| 50 | 7.72 |
（血球体积，ｍｍ），
（红血球数，百万）
(1) 画出上表的散点图;
(2)求出回归直线并且画出图形；
(3)若血球体积为49ｍｍ，预测红血球数大约是多少？
已知10只狗的血球体积及红血球的测量值如下：
|
ｘ |
45 |
42 |
46 |
48 |
42 |
35 |
58 |
40 |
39 |
50 |
|
y |
6.53 |
6.30 |
9.25 |
7.50 |
6.99 |
5.90 |
9.49 |
6.20 |
6.55 |
7.72 |
ｘ（血球体积，ｍｍ），ｙ（血红球数，百万）
(1)画出上表的散点图;(2)求出回归直线并且画出图形。