题目内容
15. 如图,四棱锥S-ABCD中,SA=SD=BC,底面ABCD为正方形,且平面SAD⊥平面ABCD,M,N分别是AB,SC的中点.
如图,四棱锥S-ABCD中,SA=SD=BC,底面ABCD为正方形,且平面SAD⊥平面ABCD,M,N分别是AB,SC的中点.(1)求证:MM∥平面SAD;
(2)求二面角S-CM-D的余弦值.
分析 (1)根据线面平行的判定定理即可证明MM∥平面SAD;
(2)建立坐标系,利用向量法求出平面的法向量,利用向量法进行求解即可.
解答 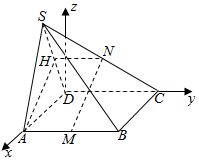 证明:(1)取SD的中点H,连接HN,MN,AH,
证明:(1)取SD的中点H,连接HN,MN,AH,
∵M,N分别是AB,SC的中点,
∴HN∥CD∥AB.
HN=$\frac{1}{2}$CD=AM,
则四边形AMNH是平行四边形,
∴AH∥MN,
∴MM∥平面SAD;
(2)∵底面ABCD为正方形,平面SAD⊥平面ABCD,
∴建立以D为坐标原点的空间直角坐标系如图:
∵SA=SD=BC,
∴设BC=1,则AD=1,
则D(0,0,0),A(1,0,0),C(0,1,0),M(1,$\frac{1}{2}$,0),S($\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),
设平面SCM的法向量为$\overrightarrow{m}$=(x,y,z),
则$\overrightarrow{CM}$=(1,$-\frac{1}{2}$,0),$\overrightarrow{CS}$=($\frac{1}{2}$,-1,$\frac{\sqrt{3}}{2}$),
由$\overrightarrow{m}$•$\overrightarrow{CM}$=0,$\overrightarrow{m}$•$\overrightarrow{CS}$=0,得$\left\{\begin{array}{l}{x-\frac{1}{2}y=0}\\{\frac{1}{2}x-y+\frac{\sqrt{3}}{2}z=0}\end{array}\right.$,
令x=2,则y=4,z=2$\sqrt{3}$,则$\overrightarrow{m}$=(2,4,2$\sqrt{3}$),
同理可得平面CMD的法向量为$\overrightarrow{n}$=(0,0,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2\sqrt{3}}{1×\sqrt{{2}^{2}+{4}^{2}+(2\sqrt{3})^{2}}}$=$\frac{2\sqrt{3}}{4\sqrt{2}}$=$\frac{\sqrt{6}}{4}$,
则二面角S-CM-D的余弦值是$\frac{\sqrt{6}}{4}$.
点评 本题主要考查线面平行垂直的判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.

| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |

| A. | k<7? | B. | k≥7? | C. | k≤8? | D. | k>8? |
| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅱ)已知每辆该型号汽车的收购价格为w=0.05x2-1.75x+17.2万元,根据(Ⅰ)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润z最大?
| A. | 不存在x0∈R,x${\;}_{0}^{2}$-1=0 | B. | 存在x0∈R,x${\;}_{0}^{2}$-1≠0 | ||
| C. | 存在x0∈R,x${\;}_{0}^{2}$-1=0 | D. | 对任意的x0∈R,x${\;}_{0}^{2}$-1≠0 |
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |