题目内容
10. 已知函数f(x)为定义域为R的偶函数,当x≥0时,f(x)=2-x+2-4
已知函数f(x)为定义域为R的偶函数,当x≥0时,f(x)=2-x+2-4(1)求f(x)的解析式;
(2)作出函数f(x)的图象,并指出其单调区间和值域(不要求证明)
(3)若关于x的方程f(x)=m 有两解,求m的取值范围.
分析 (1)根据偶函数的性质可以求出x<0时的解析式,然后得到整个定义域上的函数解析式;
(2)根据题意先画出f(x)在[0,+∞)上的图象,然后根据该函数为偶函数画出另一半的图象,即可指出其单调区间和值域;
(3)结合图象,利用数形结合的思想可获解.
解答 解:(1)设x<0,则-x>0,
∵当x≥0时,f(x)=2-x+2-4
∴f(-x)=2x+2-4;
由f(x)是定义域为R的偶函数知:f(-x)=f(x),
∴f(x)=2x+2-4,(x∈(-∞,0));…(3分)
∴函数f(x)的解析式是f(x)=$\left\{\begin{array}{l}{{2}^{-x+2}-4,x≥0}\\{{2}^{x+2}-4,x<0}\end{array}\right.$.
(2)由已知得函数f(x)的图象如图所示.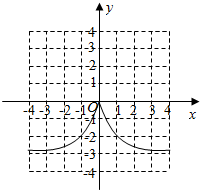
单调增区间是(-∞,0),单调减区间是(0,+∞),值域是(-4,0];
(3)由题意得:∵关于x的方程f(x)=m 有两解,
∴-3<m<0.
点评 本题考查了函数的偶函数的图象性质,以及利用图象解决方程的根的个数的问题,体现了数形结合思想的应用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
18.已知全集U={1,2,3,4,5,6},集合A={1,2},B={1,3,4,5},则集合(∁UA)∩B=( )
| A. | {1,2,3} | B. | {3,4,5,6} | C. | {3,4,5} | D. | {2,5,6} |
2.设x∈R,则“l<x<2”是“l<x<3”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |